js基础：排序算法总结

, , , ,

各样的排序算法，每次都忘记，直接手写一遍，加强记忆。

demo

https://github.com/laputaz/sort

战前准备

定义一堆数组

1
2
3
let arrs = [
  1, 356, 7, -234, 7, 24, 78678, 2342, 8, 2, 9, -56, 35, -67, 894534, 85,
]

注意

注意，我们不要一开始就纠结于循环的时候，是写 < 呢，还是 <= 。这无非就是多算一次，我们只有按照思路写出来之后再去调试，不要想着一蹴而就。

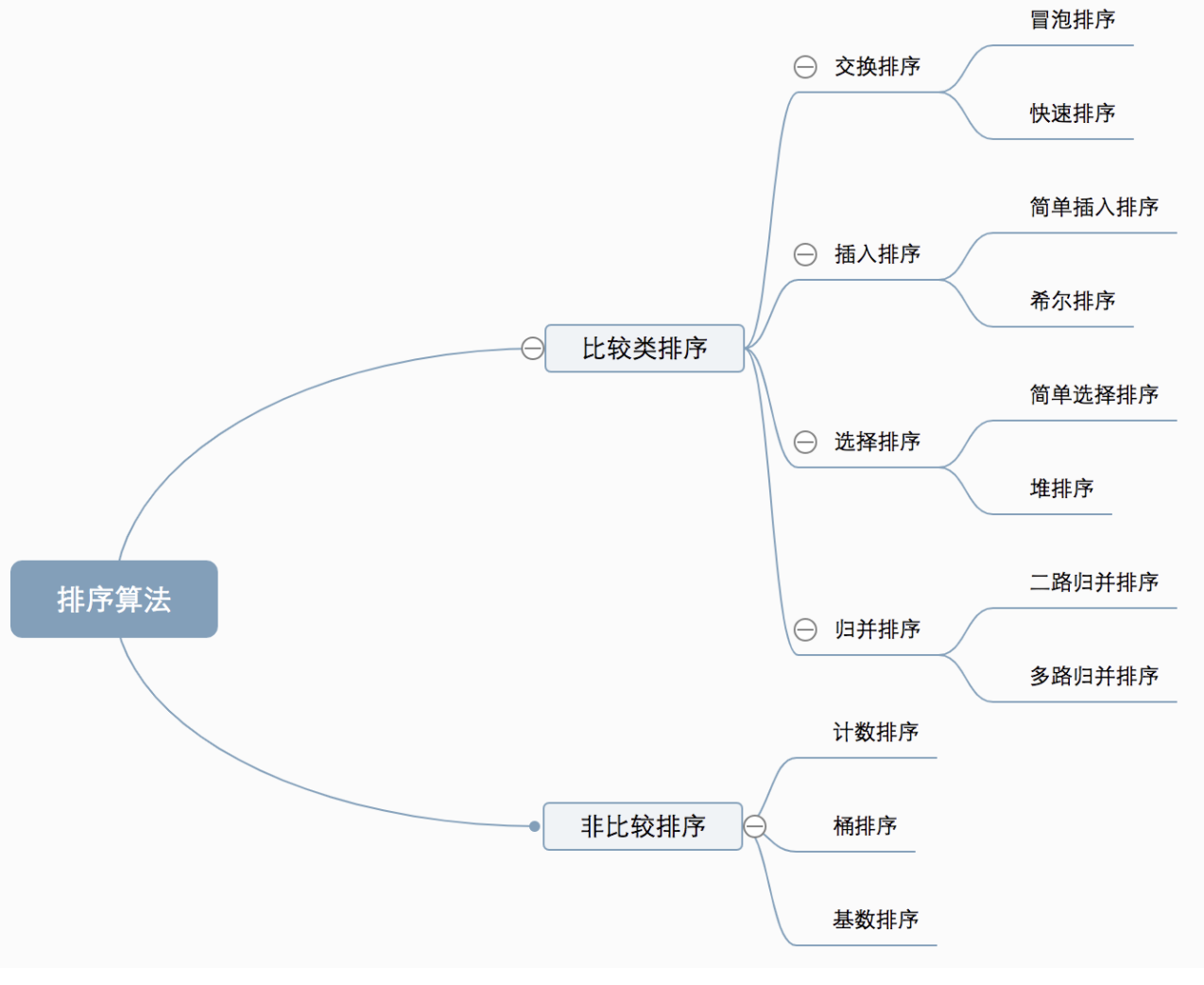
分类

常见排序算法可以分为两大类：

  • 比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破 O(nlogn)，因此也称为非线性时间比较类排序。
  • 非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。

相关概念:

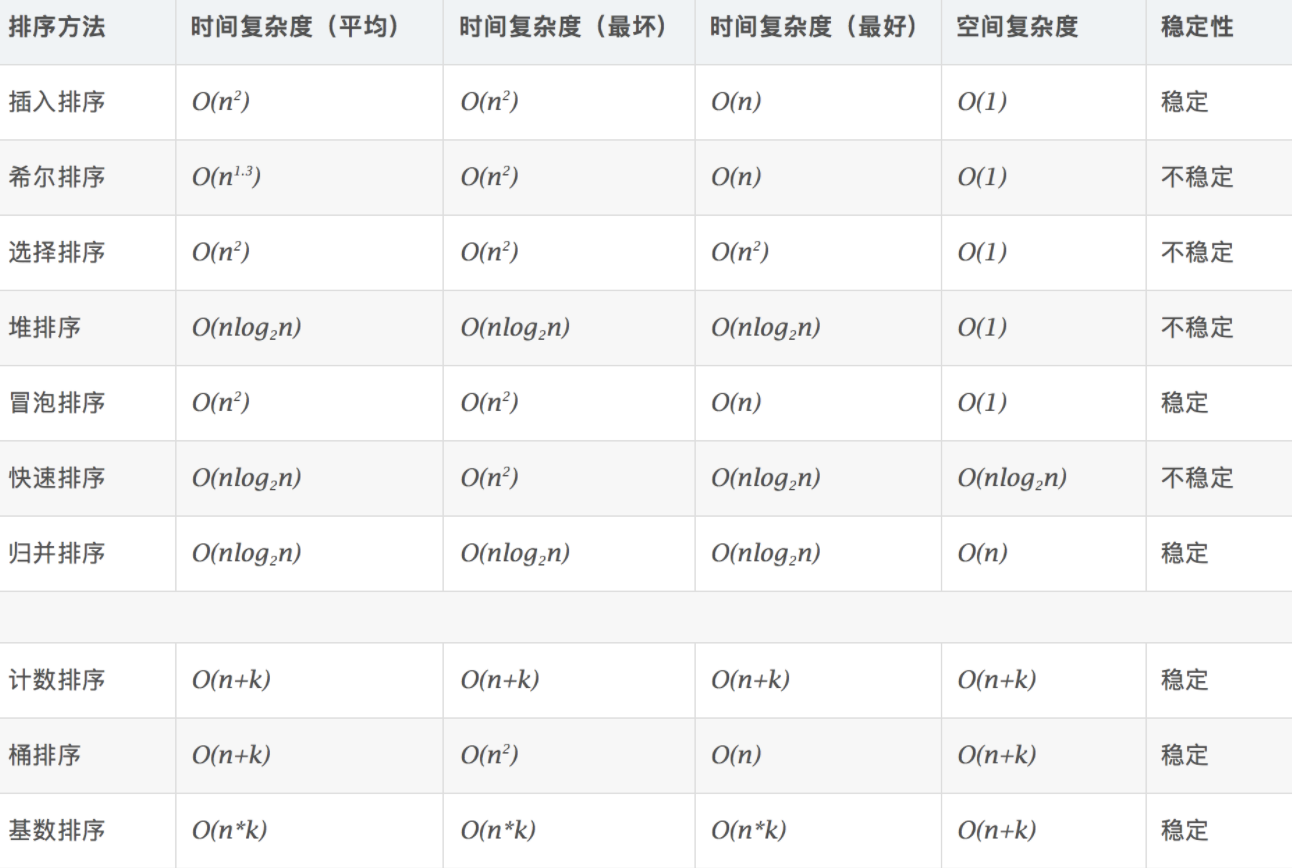
  • 稳定性：如果两个相同的数，排序之后相对位置不变，那就是稳定的。
  • 时间复杂度：对排序数据的总的操作次数。一般是规模在 n 时，需要进行的操作次数，用 n 为变量的表达式表示。
  • 空间复杂度：是指执行时所需存储空间度量，也是数据规模 n 的函数。

冒泡排序

  • 比较相邻的元素。如果第一个比第二个大，就交换它们两个；
  • 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；
  • 针对所有的元素重复以上的步骤，除了最后一个；
  • 重复步骤 1~3，直到排序完成。

代码：（双循环，一开始循环到底，每冒泡完一遍，-1）

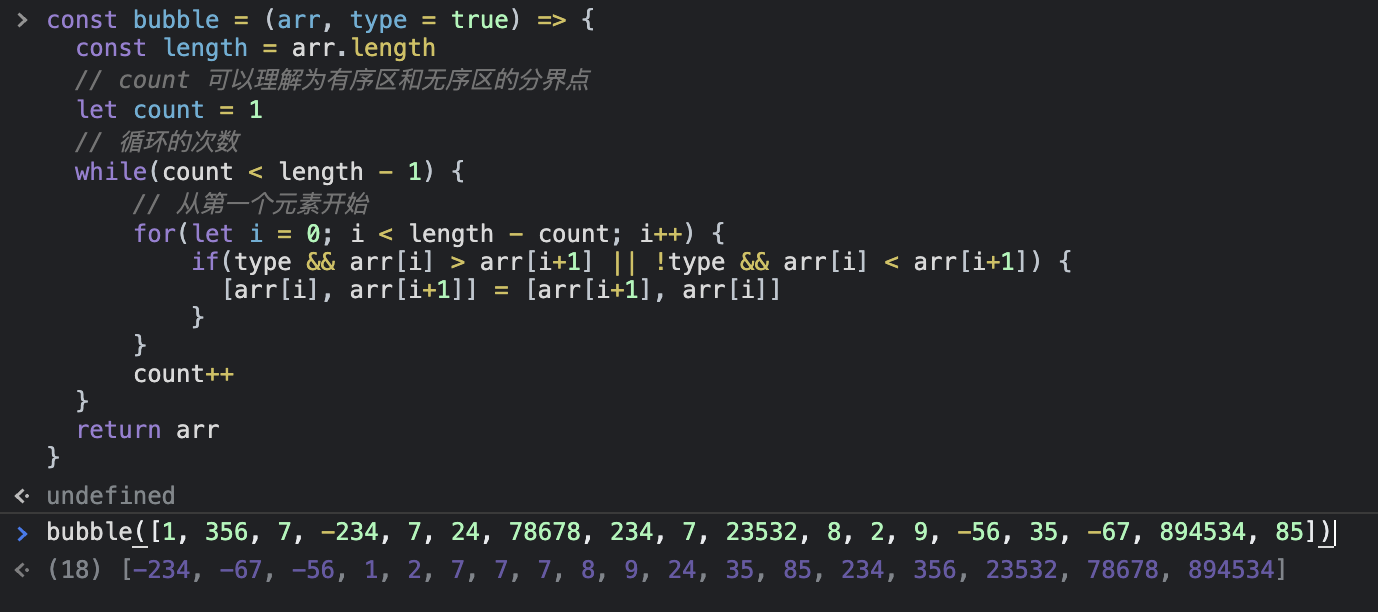
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//冒泡type升降序true升
const bubble = (arr, type = true) => {
  const length = arr.length
  // count 可以理解为有序区和无序区的分界点
  let count = 1
  // 循环的次数
  while (count < length - 1) {
    // 从第一个元素开始
    for (let i = 0; i < length - count; i++) {
      if ((type && arr[i] > arr[i + 1]) || (!type && arr[i] < arr[i + 1])) {
        ;[arr[i], arr[i + 1]] = [arr[i + 1], arr[i]]
      }
    }
    count++
  }
  return arr
}

效果：

冒泡排序的优化:

  • 外层循环优化：增加一个标志位，如果在一次外循环的冒泡中，发现没有一次交换，说明已经是有序的了，标志位置为 true,下次循环开始时直接返回。不用继续往下走了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// 冒泡之外循环优化
const bubble = (arr, type = true) => {
  const length = arr.length
  // count 可以理解为有序区和无序区的分界点
  let count = 1
  // 循环的次数
  while (count < length - 1) {
    // 终止条件
    let flag = false
    // 从第一个元素开始
    for (let i = 0; i < length - count; i++) {
      if ((type && arr[i] > arr[i + 1]) || (!type && arr[i] < arr[i + 1])) {
        ;[arr[i], arr[i + 1]] = [arr[i + 1], arr[i]]
        flag = true
      }
    }
    // 未发生交换，直接结束
    if (!flag) {
      console.log(count) // 把次数打印出来
      break
    }
    count++
  }
  return arr
}
  • 内循环优化：记住最后一次发生交换的位置，那么这个位置就是有序区和无序区的分水岭，下一次就不用再继续往后循环了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// 冒泡之内循环优化
let bubble = (arr, type = true) => {
  const length = arr.length
  // count 可以理解为有序区和无序区的分界点
  let count = 1
  // 最后一次发生交换的index, 初始是最后一个
  let lastExchangeIndex = length - count
  // 记录位置
  let pos = 0
  // 循环的次数
  while (count < length - 1) {
    // 终止条件
    let flag = false
    // 从第一个元素开始
    for (let i = 0; i < Math.min(length - count, lastExchangeIndex); i++) {
      if ((type && arr[i] > arr[i + 1]) || (!type && arr[i] < arr[i + 1])) {
        ;[arr[i], arr[i + 1]] = [arr[i + 1], arr[i]]
        flag = true
        // 记录最后一次交换的位置
        pos = i
      }
    }
    // 只循环到无序区终点
    lastExchangeIndex = Math.min(length - count, pos)
    console.log('lastExchangeIndex', lastExchangeIndex)
    // 未发生交换，直接结束
    if (!flag) {
      console.log(count) // 把次数打印出来
      break
    }
    count++
  }
  return arr
}

由此可见:

  • 冒泡最好的情况是一次都不用交换，只进行一次外循环+一次内循环，遍历了 n 个元素 O(n)
  • 冒泡最坏的情况是每一次都交换，复杂度为 O(n2)

问题来了：冒泡最坏的情况，严格来说应该是 n + (n - 1) + (n - 2) + … 1 次，为什么说是 O(n2)呢？

先来看看 Big O 到底是什么：

大 O 符号（Big O notation）是用于描述函数渐进行为的数学符号。更确切地说，它是用另一个（通常更简单的）函数来描述一个函数数量级的渐近上界。在数学中，它一般用来刻画被截断的无穷级数尤其是渐近级数的剩余项；

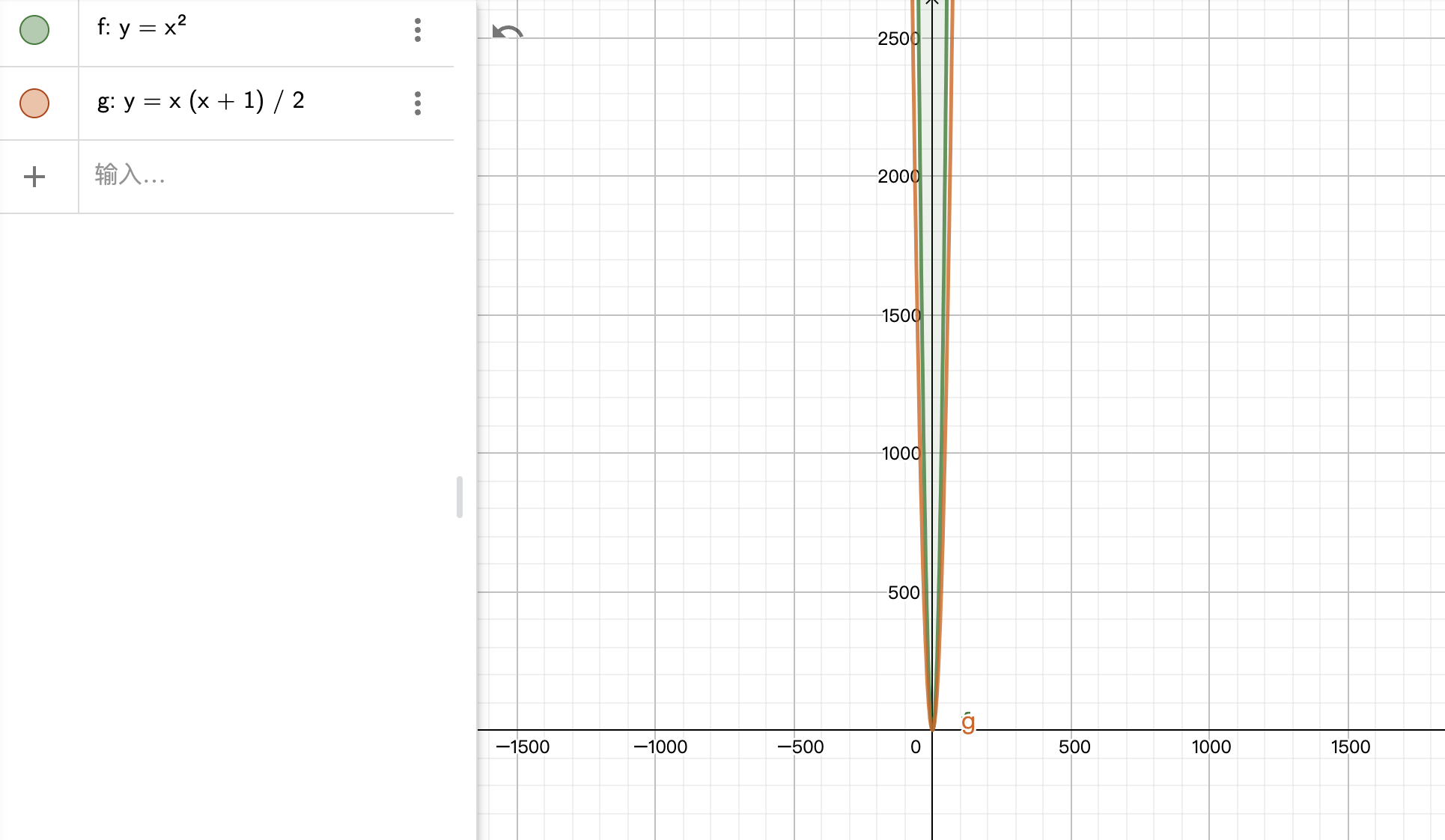
根据高中知识，其实 n + (n - 1) + (n - 2) + … 1 是累加，可以写成 n(n+1) / 2，进一步转变为 n^2 * 1/2 + n/2。
在这个式子中，当 n 足够大时，对结果起主导作用的就是 n^2。而 bigO 的规则是用最简单的式子来表示趋势的，那么用 n^2 这个主导的部分作为表示法，即 O(n2)。

在坐标轴上表示出来就很明显了，n(n+1) / 2 和 n^2 在数量够大的时候是趋近的。

选择排序

  • 初始已排序区为空，全都是未排序区
  • 每次遍历一遍，找到未排序区的最大/最小值，放在已排序区的末尾
  • 循环

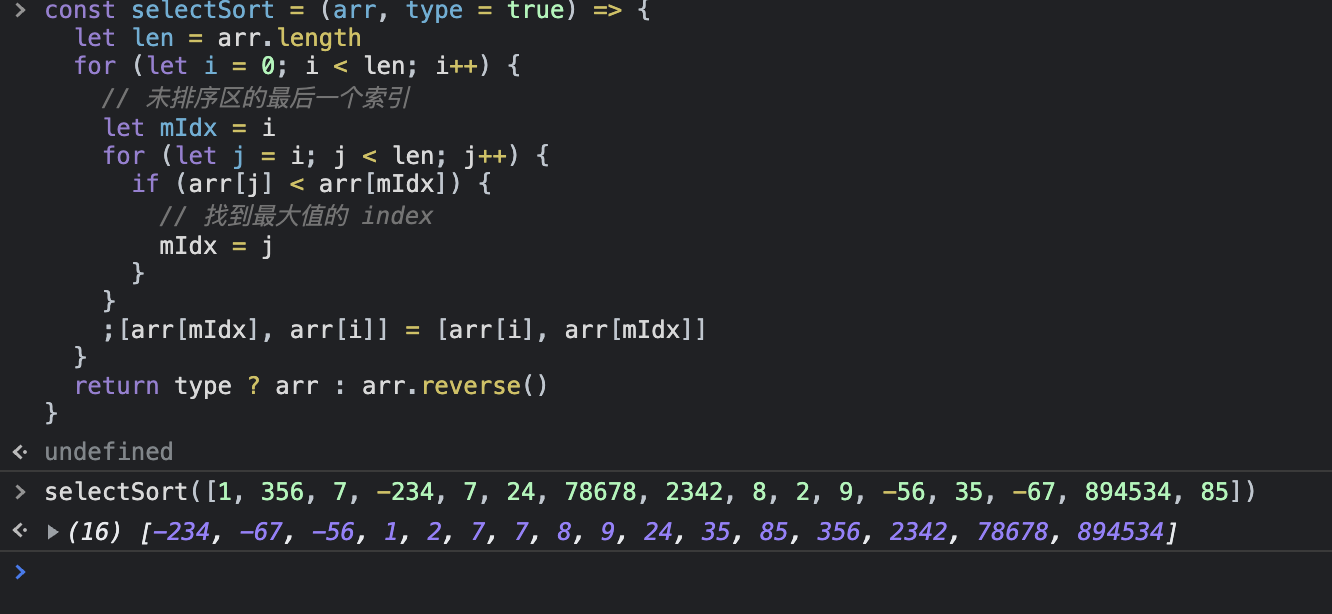
代码：（外循环为未排序区长度，内循环找最大值）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
const selectSort = (arr, type = true) => {
  let len = arr.length
  for (let i = 0; i < len; i++) {
    // 未排序区的第一个索引
    let mIdx = i
    for (let j = i; j < len; j++) {
      if (arr[j] < arr[mIdx]) {
        // 找到最大值的 index
        mIdx = j
      }
    }
    ;[arr[mIdx], arr[i]] = [arr[i], arr[mIdx]]
  }
  return type ? arr : arr.reverse()
}

结果

选择排序优化

由于我们假定了初始左半部分是已排序区，右半部分为未排序区，如图：

那其实，我们假定有两个有序区就好了

每一次遍历无序区，将最小值放在左侧，最大值放在右侧，这样可以减少循环次数。

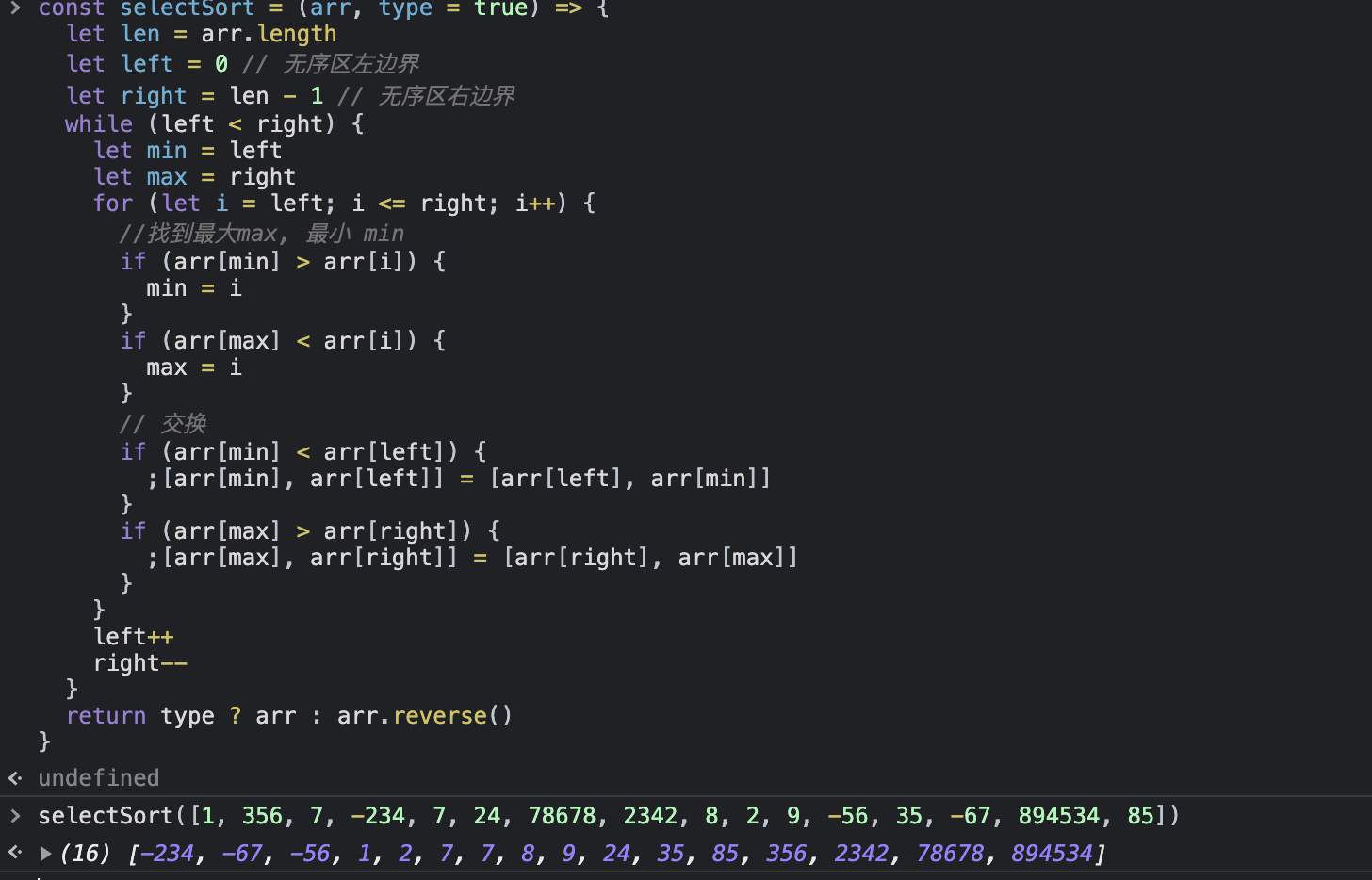
代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
const selectSort = (arr, type = true) => {
  let len = arr.length
  let left = 0 // 无序区左边界
  let right = len - 1 // 无序区右边界
  while (left < right) {
    let min = left
    let max = right
    for (let i = left; i <= right; i++) {
      //找到最大max, 最小 min
      if (arr[min] > arr[i]) {
        min = i
      }
      if (arr[max] < arr[i]) {
        max = i
      }
      // 交换
      if (arr[min] < arr[left]) {
        ;[arr[min], arr[left]] = [arr[left], arr[min]]
      }
      if (arr[max] > arr[right]) {
        ;[arr[max], arr[right]] = [arr[right], arr[max]]
      }
    }
    left++
    right--
  }
  return type ? arr : arr.reverse()
}

效果

选择排序最好和最坏都得 O(n2), 只是优化后稍微好了一点点

插入排序

  • 起始有序区是空的，剩余是无序区
  • 取出无序区的第一个元素
  • 遍历有序区，插入到有序区指定位置

其实和选择排序刚好反过来，选择排序是先在无序区比较出最大/小值，再插入到有序区末尾。
而插入排序是取出无序区第一个元素，再在有序区看看排到第几位。类似于打牌的时候整理牌。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 直接插入排序
const insert = (arr, type) => {
  const len = arr.length
  // 取出无序区第一个，i记录无序区索引最前端
  for (let i = 1; i < len; i++) {
    // 遍历有序区，找到合适的位置，再取出i, 插入
    for (let j = 0; j < i; j++) {
      if ((arr[j] > arr[i] && type) || (arr[j] < arr[i] && !type)) {
        arr.splice(j, 0, arr.splice(i, 1)[0])
        // 插入后就结束当次循环了
        break
      }
    }
  }
  return arr
}

上面是从有序区从左到右查找的过程，其实也可以从右往左查找：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
function insertSort(arr) {
  let length = arr.length
  for (let i = 1; i < length; i++) {
    let temp = arr[i]
    let j = i
    for (; j > 0; j--) {
      if (temp >= arr[j - 1]) {
        break // 当前考察的数大于前一个数，证明有序，退出循环
      }
      arr[j] = arr[j - 1] // 将前一个数复制到后一个数上
    }
    arr[j] = temp // 找到考察的数应处于的位置
  }
  return arr
}

直接插入排序最好是 O(n), 即有序的序列，最坏还是双循环 O(n2)
需要额外一个空间存储移动的元素，空间复杂度 O(1)

插入排序优化-希尔排序

插入排序有两个痛点：

  1. 当数组相对有序的时候，速度会快很多，因为插入的比较次数少了。
  2. 当数组规模很小的时候，速度会快很多

利用这两个痛点，就有了希尔排序。

  • 按照一定的跨度，将数组拆成几个子数组
  • 对每个子数组使用插入排序
  • 减少跨度，再将数组拆成几个子数组
  • 一直到跨度为 1，这个时候就是对自身执行插入排序了

也就是让将数组拆成小的规模进行插入排序，再将子数组结合起来，形成一个规模比上个阶段大一点的“相对有序”的数组（粗略调整），再执行插入排序。

将数组拆成小的规模的方式，会有一个分组的跨度。这个跨度就叫希尔增量。

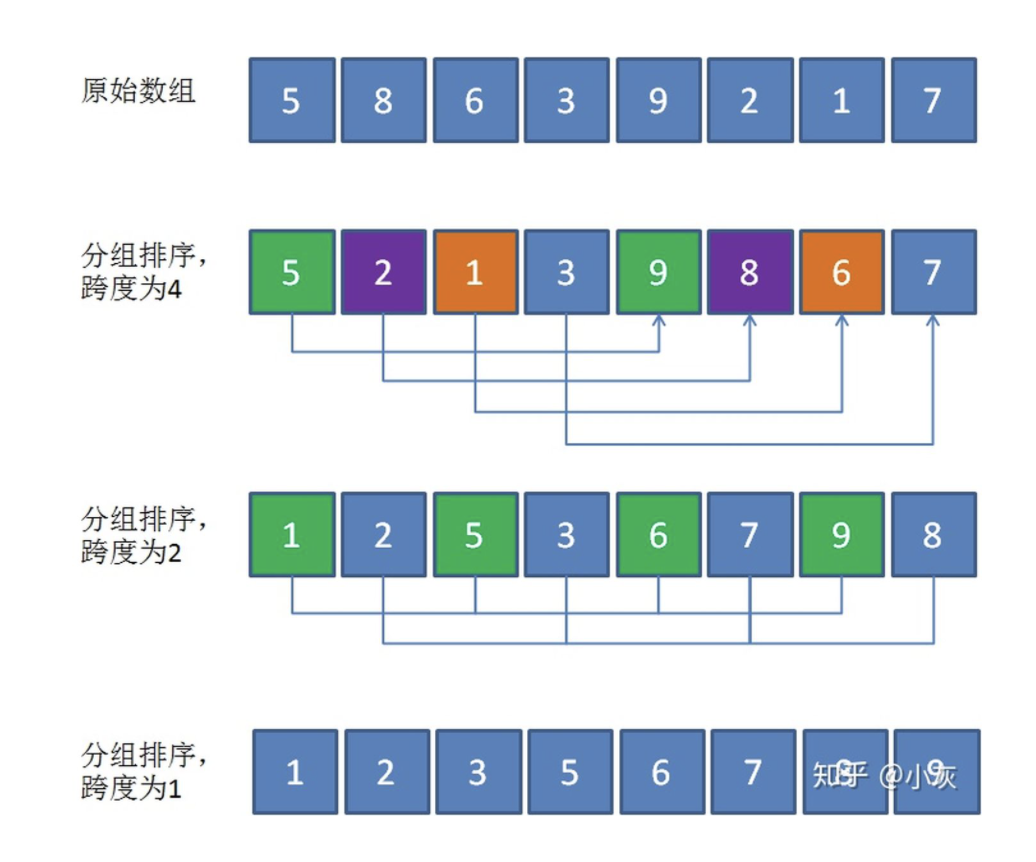
例如长度为 8 的数组：
第一次分组时，分为 [0,4], [1,5], [2,6], [3,7]一共 4 组，跨度为 4
第二次分组时，跨度为 2，分为 [0,2,4,6], [1,3,5,7]一共 2 组，跨度为 2
第三次分组时，跨度为 2，分为 [0，1，2，3，4，5，6，7]一共 1 组，跨度为 1

希尔增量，可不是只有一直除以 2 那么简单。它是一个数学问题。这里为了简单还是一直除以 2。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//希尔排序
var arr = [1, 2, 3, 41, 4, 34, 0, 76, 87]

// shellSort
const shellSort = (arr, type) => {
  const len = arr.length
  let gap = Math.floor(len / 2)
  while (gap >= 1) {
    for (let i = gap; i < len; i++) {
      let temp = arr[i]
      let j = i
      for (; j - gap >= 0 && temp < arr[j - gap]; j = j - gap) {
        arr[j] = arr[j - gap]
      }
      arr[j] = temp
    }
    gap = Math.floor(gap / 2)
  }
  return arr
}

console.log(shellSort(arr))

网络上的文章很不负责任的点在于，只解释了分组的概念，然后就仍一段代码给你，完全不解释代码的思路，看着就生气。

首先，上面这段代码的比较思路是从右往左
第二，是遍历每个元素，判断每个元素在哪个分组中，并不是一次性将分组比较完，而是先比较分组一的前面一部分，在比较分组二的前一部分，直到遍历完所有分组的前一部分；再遍历第一个分组的第二部分，第二个分组的第二部分，以此类推。

插入排序优化-二分查找插入排序

为了减少插入的比较次数，在插入的过程引入二分查找法。
二分查找的关键在于中位数。
代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// 优化插入排序
// 二分查找
const halfInsert = (arr, type = true) => {
  const len = arr.length
  let mid, low, high, pos
  // 在有序区内用二分法查找位置
  for (let i = 1; i < len; i++) {
    // 有序区最低位
    low = 0
    // 有序区最高位
    high = i - 1
    while (high > low) {
      // 找到中位, 取整
      mid = parseInt((low + high) / 2)
      // 刚好等于中位时，记录下来，结束循环，最后要插到他后边
      if (arr[i] === arr[mid]) {
        pos = mid
        break
        // 落在中位以左，将中位左侧的元素置位最高位，往左侧继续寻找
      } else if (arr[i] < arr[mid]) {
        high = mid - 1
        // 落在中位以右，将中位右侧的元素置位最低位，往右侧继续寻找
      } else {
        low = mid + 1
      }
    }
    // 循环要么找到相等的了，要么一直循环到 high === low
    if (high === low) {
      pos = arr[i] < arr[low] ? low : low + 1
    }
    // 取出
    let temp = arr.splice(i, 1)[0]
    // 插入
    arr.splice(pos, 0, temp)
  }
  return type ? arr : arr.reverse()
}

效果

快速排序

快排主要有两部分，分段(Partition)和递归(Recursive)。

  • 首先要找一个数字作为基准。为了方便，一般选择第 1 个数字作为基准
  • 把这个待排序的数列中小于基准的元素移动到待排序的数列的左边，把大于基准的元素移动到待排序的数列的右边。
  • 递归

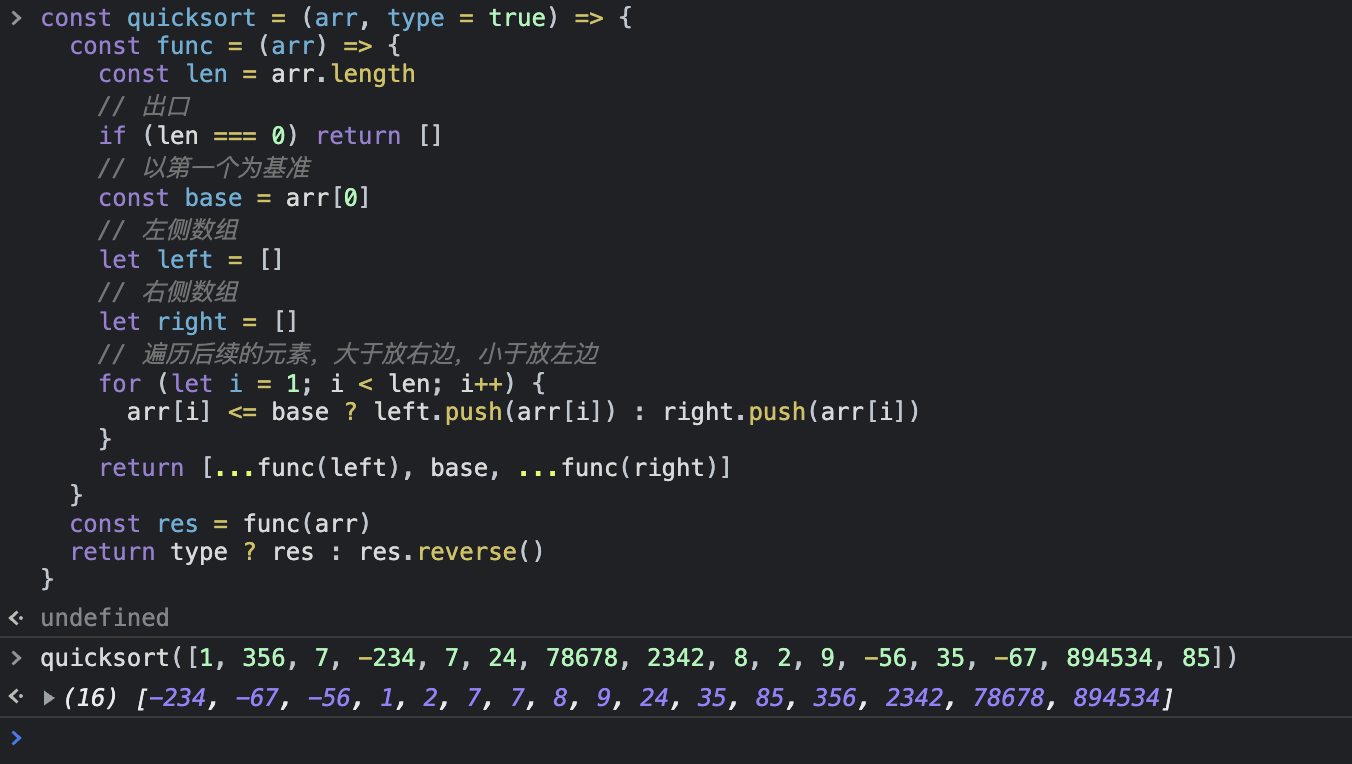
代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//快速排序
var arr = [1, 2, 3, 41, 21, 34, 23, 34, 0]

const quicksort = (arr) => {
  if (arr.length <= 1) {
    return arr
  }
  let left = []
  let right = []
  const base = arr[0]
  for (let i = 1; i < arr.length; i++) {
    if (arr[i] <= base) {
      left.push(arr[i])
    } else {
      right.push(arr[i])
    }
  }
  return [...quicksort(left), base, ...quicksort(right)]
}

console.log(quicksort(arr))

效果

快速排序优化

上面这种写法有两个问题：

  1. 用了新数组 left 和 right，数据量很大的时候，占用内存会很大，空间复杂度很高
  2. 没有递归优化，数据量大的时候调用栈过多，容易堆栈溢出

解决：

  1. 使用交换的形式，而不是开辟新数组
  2. 递归优化，减少递归深度（注意不是尾递归）
  3. 当数组是正序或者倒序的时候，性能会比较差。因为比较次数是固定的，正序或者倒序的数组，会导致某一端的调用栈过深。所以优化 pivot 的取值很重要。平衡的分区可以达到 O(nlogn) 而不是最坏的 O(n2)
    • 扫描一下整个数组，计算出一个中间值作为 pivot，让分区平衡

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// start 为待排序的起点，end为待排序终点
const quickSort = (arr, left, right) => {
  const leftIndex = left ?? 0
  const rightIndex = right ?? arr.length - 1
  if (leftIndex < rightIndex) {
    let partitionIndex = partition(arr, leftIndex, rightIndex)
    quickSort(arr, leftIndex, partitionIndex - 1)
    quickSort(arr, partitionIndex + 1, rightIndex)
  }
  return arr
}

//！ 交换方法一：先对比交换其他元素，最后再交换基准到中间。
const partition = (arr, left, right) => {
  // 以左侧为基准
  let pivot = left
  // 左右指针
  let i = left,
    j = right
  while (i < j) {
    // 从右往左
    while (arr[j] >= arr[pivot] && i < j) {
      j--
    }
    // 从右往左
    while (arr[i] <= arr[pivot] && i < j) {
      i++
    }
    ;[arr[i], arr[j]] = [arr[j], arr[i]]
  }
  // 交换基准到中间
  ;[arr[pivot], arr[i]] = [arr[i], arr[pivot]]
  // 返回基准最后的位置
  return i
}

这就是双哨兵法


为什么要从右边开始呢，因为从右开始，直到停下来，会出现：

  1. 没有一个比基准小的，停下来的位置刚好是左哨兵和基准，最后就是左哨兵等于右哨兵等于基准，不用交换，整个右边都比基准大
  2. 最后停下来的位置不是基准，而是中间的某个元素。
    • 如果最后移动的是右哨兵（说明上一步已经让左右哨兵交换过了），此时停止位一定是比基数小的，停止位右边的所有数都比基数大。这个时候交换哨兵和基数，可以保证左边都是小的，右边都是大的。
    • 如果最后移动的是左哨兵，此时右哨兵在的位置肯定也是比基数小的，因为右哨兵停下来的位置就是第一个比基数小的位置。那么停止位右边的数都比基数大，左边都比基数小，同理。

例子：可以用 6，1，2，7，9 走走看，从左往右的话，7 和 6 互换，就是错的。

从右往左可以保证最后停下来的数要小于基数，从左往右可能会出现停下的数大于基数的情况。

递归优化，减少递归深度

把入口代码改成

1
2
3
4
5
6
7
8
9
// start 为待排序的起点，end为待排序终点
const quickSort = (arr, left, right) => {
  let pivot = left
  while (left < right) {
    pivot = partition(arr, left, right)
    quickSort(arr, left, pivot - 1)
    left = pivot + 1
  }
}

这种方法相当于在一个调用内尽可能多地调用自身。增加广度，减少深度。并不算尾递归调用。看这里

=>

另外的优化点

扫描一下整个数组，计算出一个中间值作为 pivot，让分区平衡
分割策略：随机取数法和三数取中。其实都是为了保证分割相对平衡，而不是严重失衡。

归并排序

把数组一直对半划分，划分到最小粒度的时候，开始进行两两有序数组的合并。

  • 把长度为 n 的输入序列分成两个长度为 n/2 的子序列；
  • 对这两个子序列分别采用归并排序；
  • 将两个排序好的子序列合并成一个最终的排序序列。

归并排序始终都是 O(nlogn）的时间复杂度。代价是需要额外的内存空间。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
//归并排序
const merge = (left, right) => {
  let arr = []
  // 两个数组都有长度时
  while (left.length && right.length) {
    if (left[0] <= right[0]) {
      arr.push(left.shift())
    } else {
      arr.push(right.shift())
    }
  }
  if (left.length) {
    arr = [...arr, ...left]
  }
  if (right.length) {
    arr = [...arr, ...right]
  }
  return arr
}
// 归并
const mergeSort = (arr, type) => {
  let len = arr.length
  // 长度小于2，直接返回
  if (len < 2) return arr
  // 切分
  let mid = Math.floor(len / 2)
  let left = arr.slice(0, mid)
  let right = arr.slice(mid)
  // 递归
  return type
    ? merge(mergeSort(left), mergeSort(right))
    : merge(mergeSort(right), mergeSort(left))
}

计数排序

计数排序要求输入的数据必须是有确定范围的整数。O(n+k)

  • 找出最大最小值
  • 建立一个长度为最大值的统计数组，每项数字都为 0
  • 遍历原始数组，将值作为索引，元素出现次数作为值
  • 遍历统计数组，push 进出现次出个元素，索引作为值

计数排序的缺点在于浪费空间，例如一个数组，大部分值都落在 1-1000，只有一两个在 10000+，那么 1000~10000 中间的存储就被浪费了。亦或者大部分元素都在 100~200，那 0~100 的部分就被浪费了。所以优化点在于不知要拿到最大值，还要拿到最小值。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function countingSort(arr, maxValue) {
  // 建立统计数组
  var bucket = newArray(maxValue + 1).fill(0),
    sortedIndex = 0,
    arrLen = arr.length,
    bucketLen = maxValue + 1
  for (var i = 0; i < arrLen; i++) {
    bucket[arr[i]]++
  }
  for (var j = 0; j < bucketLen; j++) {
    while (bucket[j] > 0) {
      arr[sortedIndex++] = j
      bucket[j]--
    }
  }
  return arr
}

桶排序

桶排序是计数排序的升级版。

  • 根据自定规则划分 n 个桶
  • 每个桶内执行排序(有可能再使用别的排序算法,或是以递归方式继续使用桶排序进行排)
  • 合并桶

规则的指定很重要，需要尽量保证每个桶之间是均匀的，避免出现空桶或者数量差异极大的桶。因为差异极大的话跟没分桶有什么区别？桶的思路就是用空间换取时间。数要相对均匀分布，桶的个数也要合理设计。其实我觉得应该叫分类排序。

假设排序的序列取值范围为 [0, 99]，我们选定十位数作为桶的映射函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
function BucketSort(list) {
  const buckets = []
  for (let i = 0; i < list.length; i++) {
    const digit = parseInt(list[i] / 10)
    if (!buckets[digit]) {
      buckets[digit] = []
    }
    insert(buckets[digit], list[i])
  }
  let p = 0
  for (let i = 0; i < buckets.length; i++) {
    if (buckets[i]) {
      while (buckets[i].length) {
        list[p++] = buckets[i].shift()
      }
    }
  }
  return list
}
function insert(list, n) {
  let i = list.length
  for (; i > 0; i--) {
    if (list[i - 1] > n) {
      list[i] = list[i - 1]
    } else {
      break
    }
  }
  list[i] = n
}

基数排序

原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。

  • 将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零
  • 从最低位开始，依次进行一次排序
  • 从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列

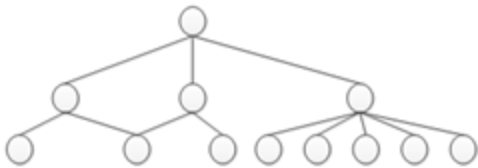
例如有

1
arr = [6, 4322, 432, 344, 55]

前面补上 0 ，变为

1
arr = [0006, 4322, 0432, 0344, 0055]

第一次,根据个位数分桶。

按照顺序来进行回收：结果：[4322,432,344,55,6]

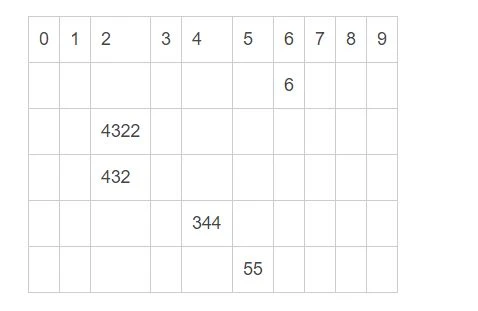
第二次，根据十位数分桶

按照顺序来进行回收：结果：[6,4322,432,344,55]

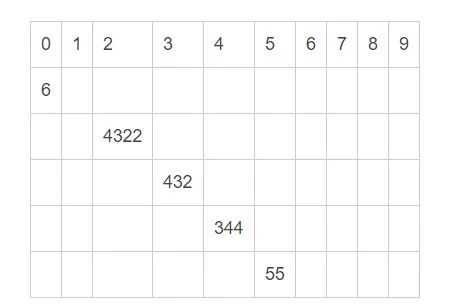
第三次，根据百位数分桶

按照顺序来进行回收：结果：[6,55,4322,344,432]

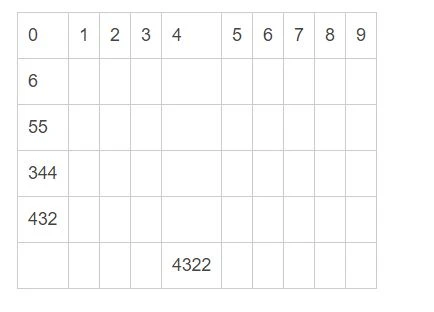
第四次，根据千位数分桶

按照顺序来进行回收：结果：[6,55,344,432,4322]

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 省略获取位数的步骤，直接传参
function RadixSort(list, maxDigit) {
  const counter = []
  for (let digit = 0, mod = 10; digit < maxDigit; digit++, mod *= 10) {
    for (let i = 0; i < list.length; i++) {
      const radix = parseInt((list[i] % mod) / (mod / 10))
      if (!counter[radix]) {
        counter[radix] = []
      }
      counter[radix].push(list[i])
    }
    let p = 0
    for (let i = 0; i < counter.length; i++) {
      if (counter[i]) {
        while (counter[i].length) {
          list[p++] = counter[i].shift()
        }
      }
    }
  }
  return list
}

堆排序

利用大小顶堆的特性，移动元素

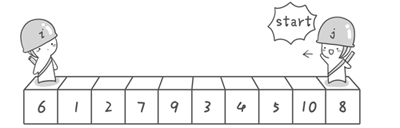
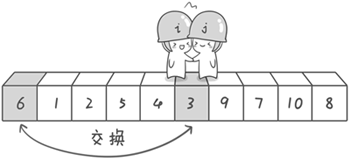
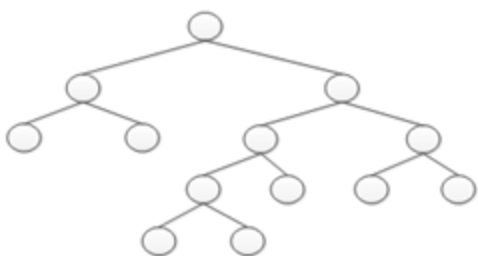  • 版权声明： 本博客所有文章除特别声明外，均采用 CC BY 4.0 CN协议 许可协议。转载请注明出处！

Laputa Z

Жизнь, как качели - то вверх, то вниз.