最近复习了一下算法,决定记录一下。算法并不是不能记忆。很多时候会发现即使理解了,也写不出来。其实有大量大量的模板,可以进行记忆,形成快速反应,再进行修改。
复杂度
即输入为 n 时,需要计算的次数:
在坐标轴的对比: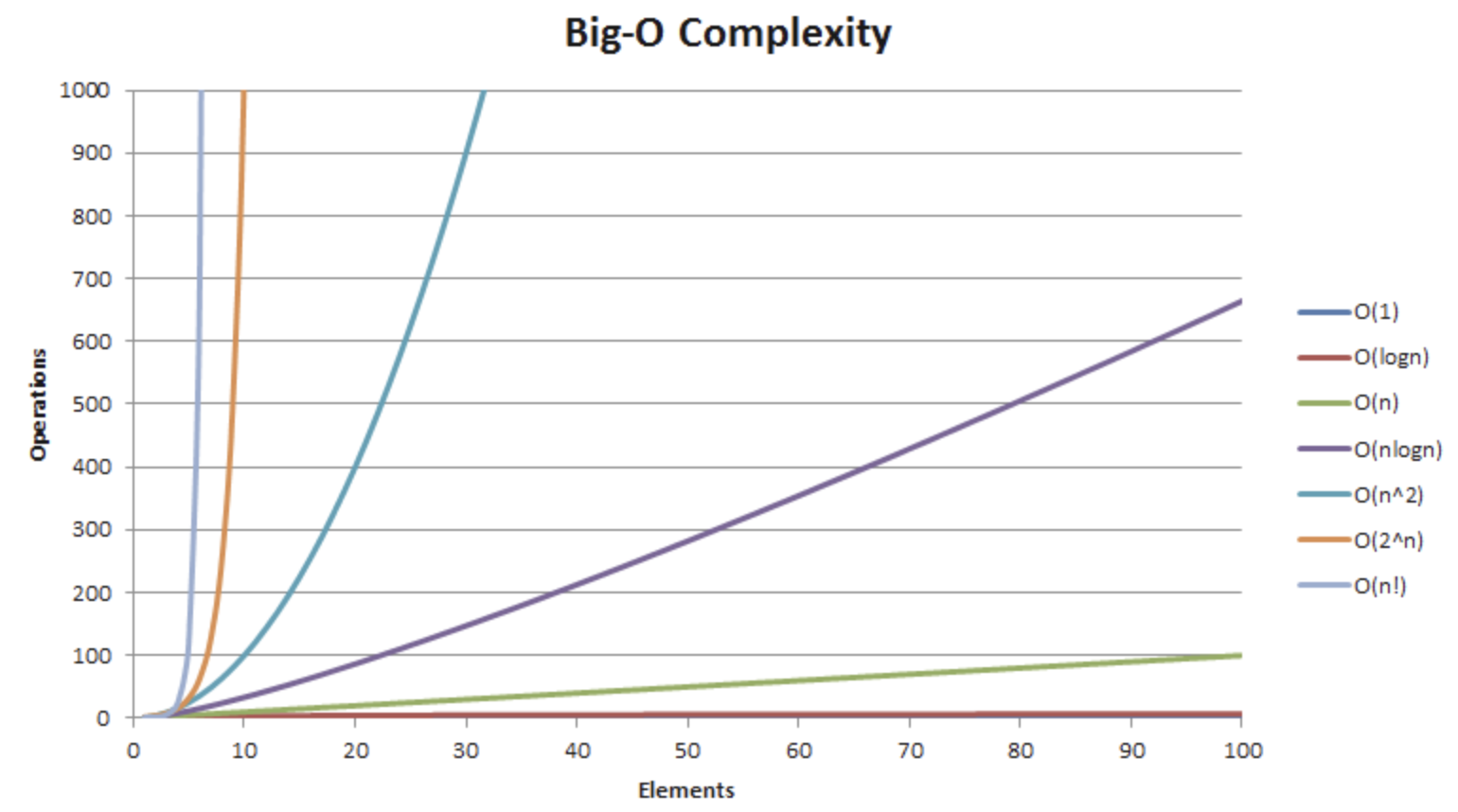
大 O 符号(Big O notation)是用于描述函数渐进行为的数学符号。更确切地说,它是用另一个(通常更简单的)函数来描述一个函数数量级的渐近上界。在数学中,它一般用来刻画被截断的无穷级数尤其是渐近级数的剩余项;
bigO 的规则是用最简单的式子来表示趋势的,所以不要纠结例如双循环是 n(n-1) 而不是 n^2 。
因为 n(n-1) => n^2 - n, n^2 是这个式子的主导部分,作为表示法,即 O(n2)。
当数据规模很大的时候,效率的差距还是很明显的。
原理实现类
此类算法通常是需要让你实现、复现已有的功能:
- 迭代器实现 - 让 obj 支持 for of
1 | const obj = { a: 1, b: 2, c: 3 }; |
- promise 实现
1 | // MyPromise.js |
- 实现 new
1 | function newObject() { |
- instanceof
1 | const instance_of = (left, right) => { |
数据结构
每种数据结构都有优缺点,需要运用在合适的场景才能发挥出最大的优势。不会有哪一种数据结构是万能的。
数组&链表
数组:可以根据索引直接查询(一般是连续的内存空间,所以插入的时候需要后挪,插入效率不好)
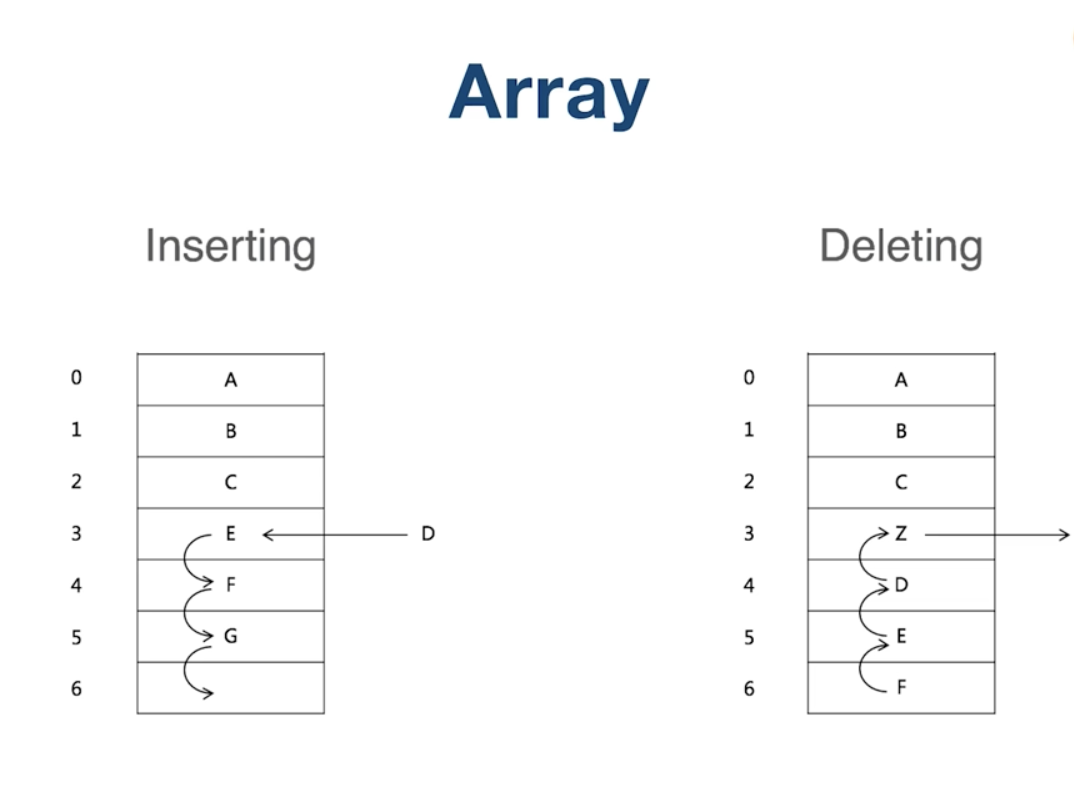
- 查询复杂 O(1)
- 插入复杂最好 O(1)(插入到最后),最坏 O(n)(插入到最前面),平均复杂下来 O(n)
链表:改善数组的插入操作
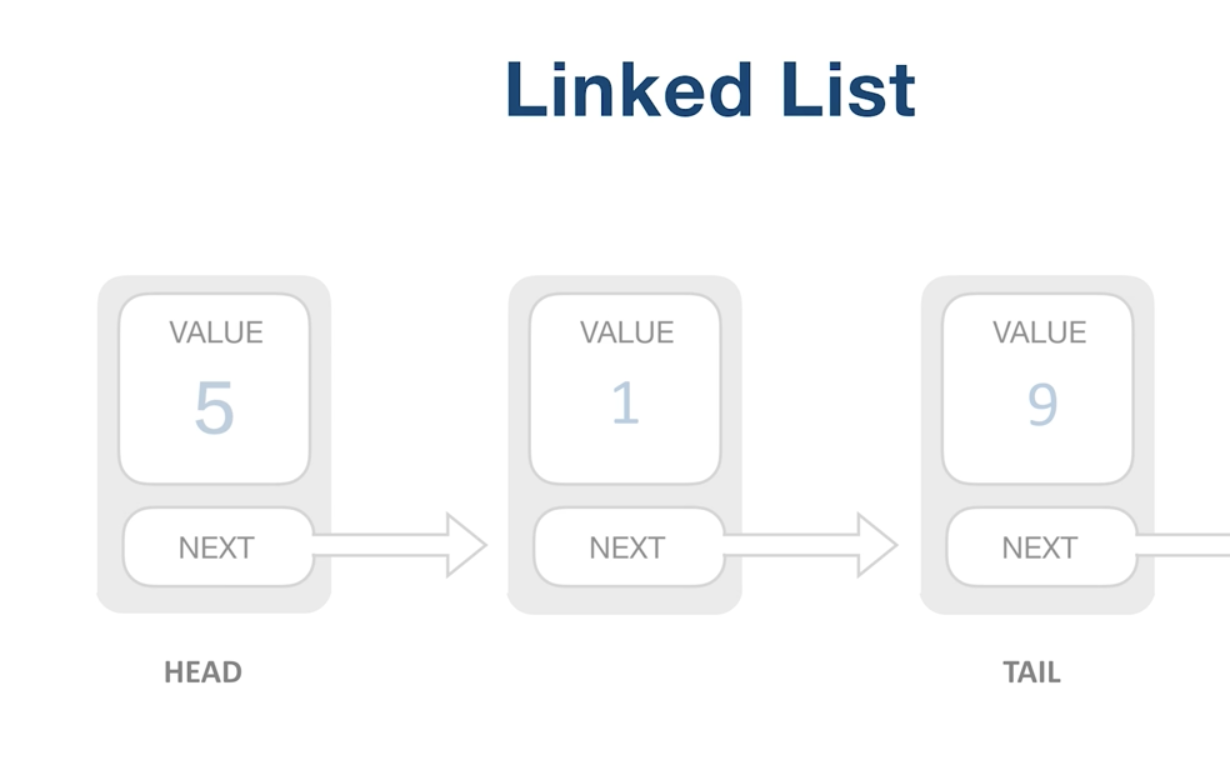
- 查询复杂 O(n) 遍历
- 插入复杂 O(1),只需要改变指针的指向,常数级操作
链表实现
首先,细粒度每个链表节点的特点
- 有 value 记录自身。
- 有 next 指向下一个节点。
整个链表的基本特点
- size 长度
- head 头指针位置
- tail 尾指针
- find(index) 查找,从 head 开始遍历
- prepend(value) 向头添加节点
- append(value) 按顺序加值
- pop() 删除并返回最后一个
- shift() 删除并返回第一一个
- insert(value, index) 向单链表指定位置后插入
- remove(index) => 在单链表中删除一个节点
- clear() => 清空单链表
1 | // 节点 |
1 | const list = new LinkedList(); // LinkedList {size: 0, head: null, tail: null} |
- 反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表头。leetcode 206

1 | /** |
两两交换链表中的节点 leetcode 24
- 递归法 => 两个指针,p 和 q,q 指向 p,p 连接后面要交换的子链表
1
2
3
4
5
6
7
8
9
10
11const swapPairs = (head) => {
if (head === null || head.next === null) {
return head;
}
let p = head;
let q = p.next;
let temp = q.next;
q.next = p;
p.next = swapPairs(temp);
return q;
};- 迭代法 => 三个指针,一直交换
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
const swapPairs = (head) => {
if (!head || !head.next) {
return head;
}
let result = head.next;
let p = head;
let temp = p.next;
let fakeHead = new ListNode(-1);
while (p.next) {
p.next = temp.next;
temp.next = p;
fakeHead.next = temp;
fakeHead = p;
p = p.next;
if (!p) {
break;
}
// 交换完了之后
temp = p.next;
}
return result;
};判断链表是否有环 leetcode 141
- 标记法,每遍历一个节点,set 记录内存地址。(O(n) 遍历一遍)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16var hasCycle = function (head) {
if (!head || !head.next) {
return false;
}
let p = head;
p.flag = 1;
while (p != null && p.next != null) {
p = p.next;
if (p.flag) {
return true;
} else {
p.flag = 1;
}
}
return false;
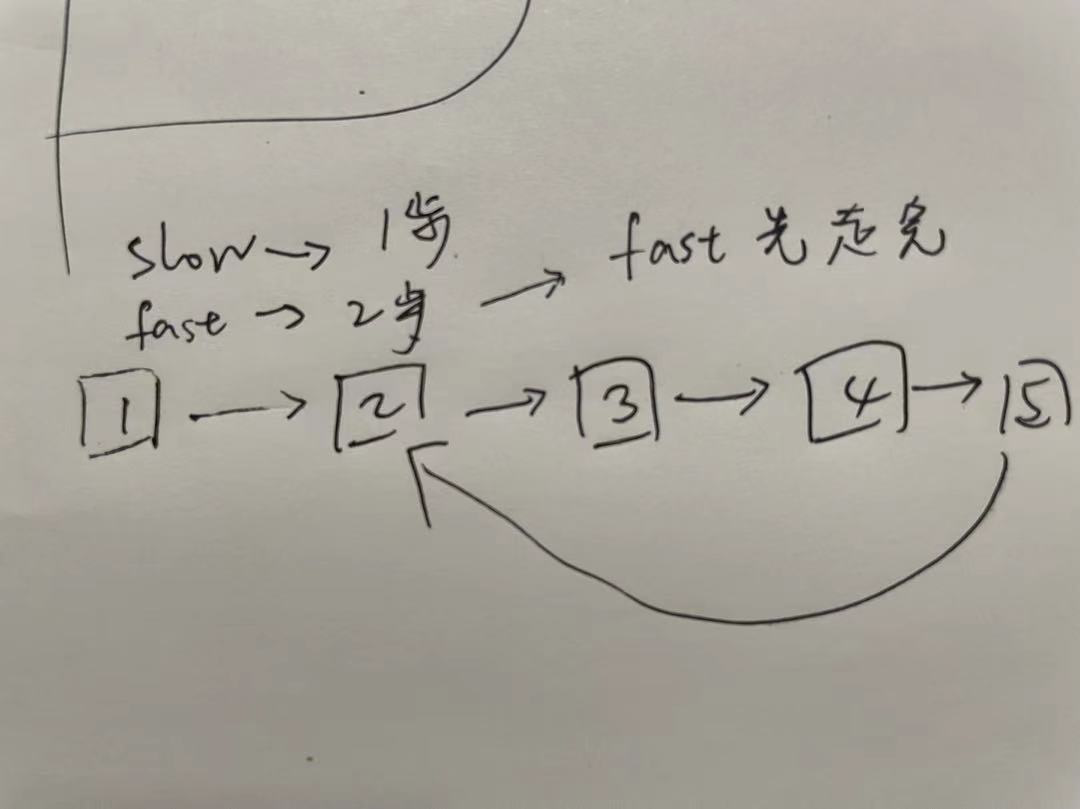
};- 快慢指针,1 步走和两步走,有环的话肯定会相撞。(O(n) 遍历一遍)
1
2
3
4
5
6
7
8
9
10var hasCycle = function (head) {
let p = head;
let q = head;
while (q != null && q.next != null) {
p = p.next;
q = q.next.next;
if (p === q) return true;
}
return false;
};- 如果要知道环的起点,具体位置,leetcode 142
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var detectCycle = function (head) {
let pos = null;
if (!head || !head.next) {
return pos;
}
pos = head;
let set = new Set();
set.add(pos);
while (pos && pos.next) {
pos = pos.next;
if (set.has(pos)) {
return pos;
}
set.add(pos);
}
return null;
};
栈和队列
栈:先进后出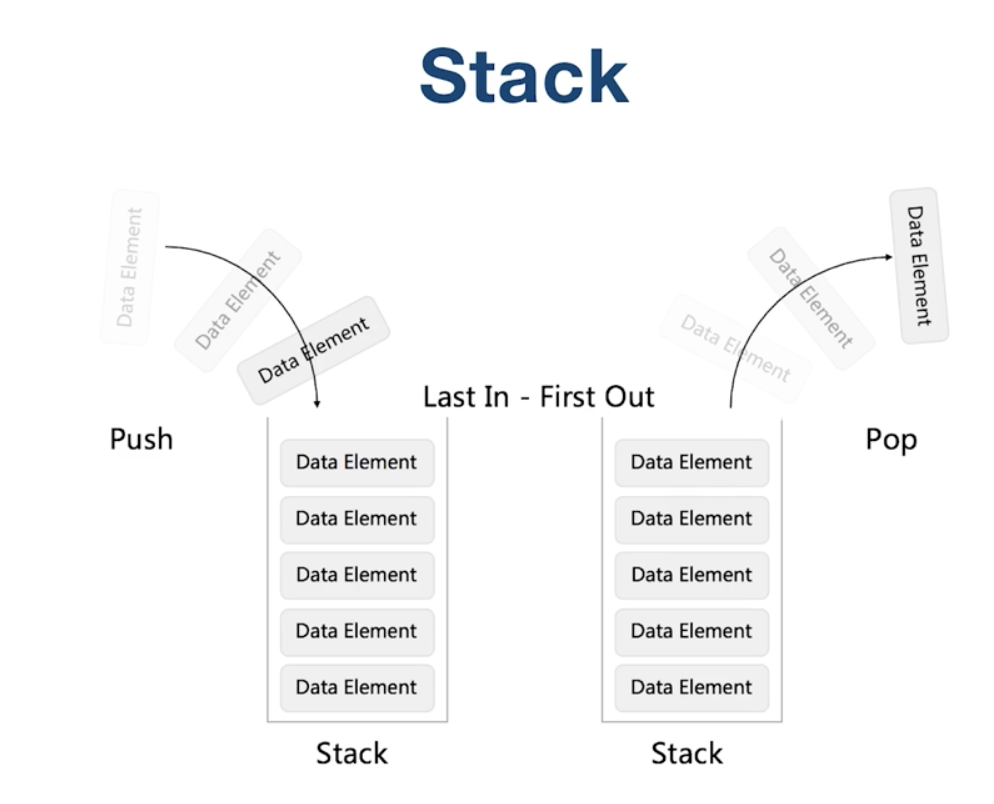
- 查找 O(n)
- 插入 O(1)
队列:先进先出
- 查找 O(n)
- 插入 O(1)
leetcode 20,包含大中小括号的字符串,判断字符串是否有效
- 用进栈出栈解决,最后栈为空。O(n) 最好用 map 把左右括号映射关系存起来。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16var isValid = function (s = '') {
let arr = [];
const map = {
'}': '{',
')': '(',
']': '[',
};
Array.prototype.forEach.call(s, (v) => {
if (!map[v] || arr[arr.length - 1] !== map[v]) {
arr.push(v);
} else {
arr.pop();
}
});
return !arr.length;
};- 不断 replace(“()”, “”)消除,一直到为空。但因为 replace 查找的操作也需要遍历,可能时间复杂度会达到 n^2
1
2
3
4
5
6var isValid = function (s = '') {
while (s.includes('{}') || s.includes('[]') || s.includes('()')) {
s = s.replace('{}', '').replace('[]', '').replace('()', '');
}
return !s.length;
};leetcode 232,225。用栈实现队列
- 用一个输入栈和输出栈,当执行取出时,从输出栈输出,若输出栈为空,从输入栈读取过来,再取出。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59var MyQueue = function () {
this.inarr = [];
this.outarr = [];
};
/**
* @param {number} x
* @return {void}
*/
MyQueue.prototype.push = function (x) {
this.inarr.push(x);
};
/**
* @return {number}
*/
MyQueue.prototype.pop = function () {
this.fill();
return this.outarr.pop() || null;
};
/**
* @return {number}
*/
MyQueue.prototype.peek = function () {
this.fill();
return this.outarr[this.outarr.length - 1] || null;
};
/**
* @return {boolean}
*/
MyQueue.prototype.empty = function () {
this.fill();
console.log(this.outarr);
if (!this.outarr.length) {
return true;
}
return false;
};
/**
* @return {boolean}
*/
MyQueue.prototype.fill = function () {
if (!this.outarr.length) {
while (this.inarr.length) {
this.outarr.push(this.inarr.pop());
}
}
};
/**
* Your MyQueue object will be instantiated and called as such:
* var obj = new MyQueue()
* obj.push(x)
* var param_2 = obj.pop()
* var param_3 = obj.peek()
* var param_4 = obj.empty()
*/
优先队列
- 正常进,按照优先级出
实现机制
- 堆 (查找最大、最小总是 O(1), 插入需要看堆的具体实现)
- 堆中某个结点的值总是不大于或不小于其父结点的值;
- 堆总是一棵完全二叉树。(若设二叉树的深度为 h,除第 h 层外,其它各层 (1 ~ h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。)
- 二叉搜索树
leetcode 703。数据流中第 k 大的元素
- 保存前 k 个最大值。每次进来一个元素排序依次 O(n*klogk)
1
2
3
4
5
6
7
8
9var KthLargest = function (k, nums = []) {
this.nums = nums;
this.k = k;
};
KthLargest.prototype.add = function (val) {
this.nums.push(val);
return this.nums.sort((a, b) => b - a)[this.k - 1];
};- 小顶堆,size = 3, 每次进来一个元素跟最小的比较(O(n)),比顶小,则取顶。比顶大,则删掉顶,加入新元素,重排堆(logk)。则最后为 O(n*logk)
leetcode 239。滑动窗口最大值 size=3。
- 暴力,每次都排序一次
- 维护大顶堆(删除新元素,查找顶元素), size 为窗口大小 3。重排堆(logk)。复杂度 O(nlogk)
- 双端队列, 关键在于双端队列记录的是索引,不是实际值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22var maxSlidingWindow = function (nums, k) {
const deque = [];
const res = [];
for (let i = 0; i < nums.length; i++) {
if (deque.length && deque[0] <= i - k) {
deque.shift();
}
// 与最右侧比较
while (deque.length) {
if (nums[deque[deque.length - 1]] < nums[i]) {
deque.pop();
} else {
break;
}
}
deque.push(i);
if (i >= k - 1) {
res.push(nums[deque[0]]);
}
}
return res;
};
映射和集合
哈希表,即,将字符串用哈希函数计算生成 key,再插入值。
如何解决哈希碰撞?在每个冲突处构建链表,将所有冲突值链入链表,如同拉链一般一个元素扣一个元素,故名拉链法。
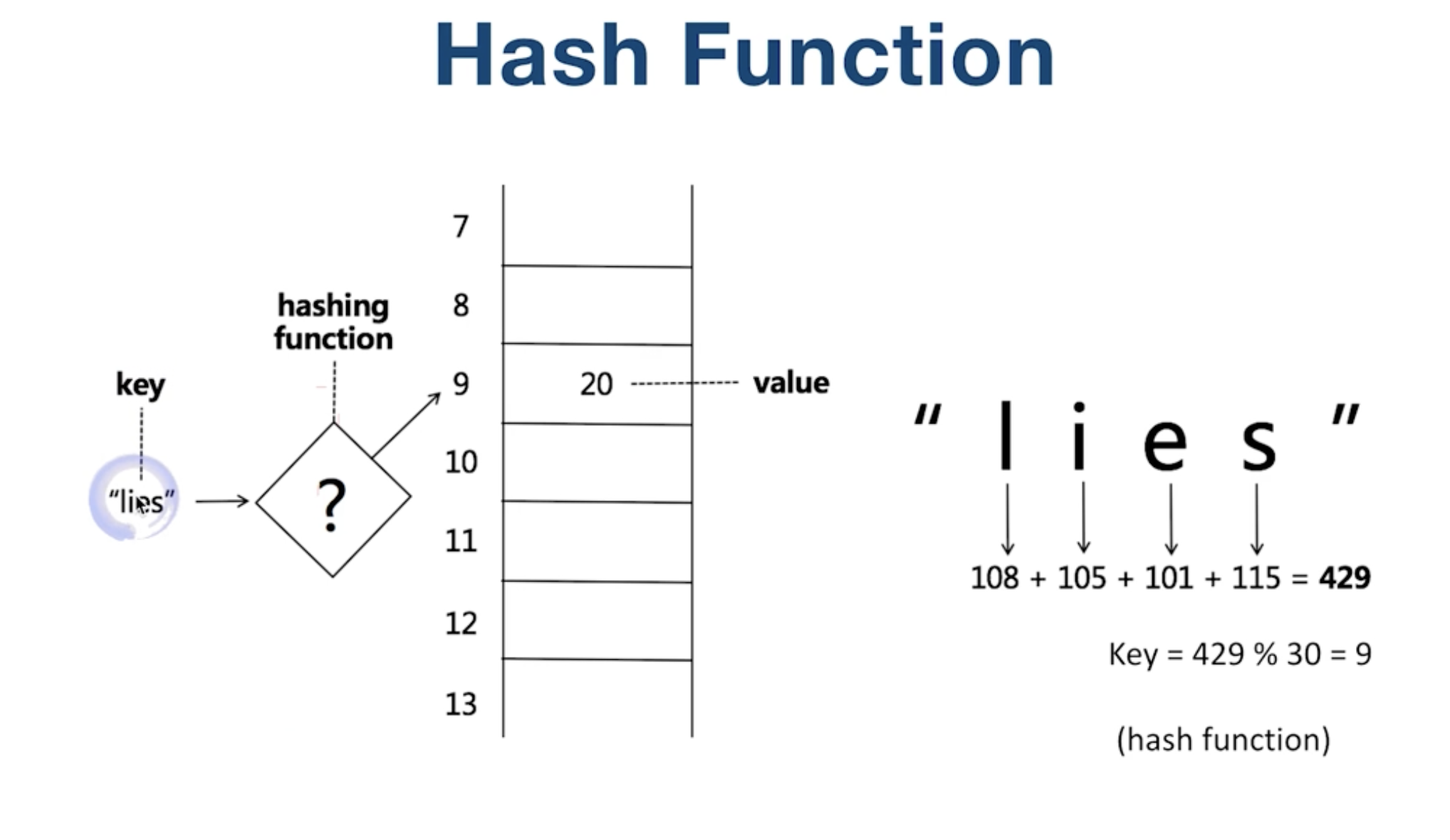

Map 和 Set 都可使用哈希表实现存储,查询插入删除速度为 O(1)。也可以用 Tree 来存储,查询速度为 O(logn),TreeMap 和 TreeSet 优势在于相对有序。
有效的字母异位词 leetcode 242
- 排序 O(nlogn)
1
2
3
4
5
6var isAnagram = function (s, t) {
/** 转换成数组排序后对比 */
s = [...s].sort();
t = [...t].sort();
return s.join('') === t.join('');
};- 用 Map 记录,最后比较(大写字母 A-Z 对应的 ASCII 码值是 65-90,小写字母 a-z 对应的 ASCII 码值是 97-122)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28var isAnagram = function (s, t) {
/** 转换成数组排序后对比 */
let a = new Map(),
b = new Map();
for (charcode of s) {
if (a.has(charcode)) {
a.set(charcode, a.get(charcode) + 1);
} else {
a.set(charcode, 1);
}
}
for (charcode of t) {
if (b.has(charcode)) {
b.set(charcode, b.get(charcode) + 1);
} else {
b.set(charcode, 1);
}
}
if (a.size !== b.size) {
return false;
}
for ([key, value] of a) {
if (b.get(key) !== value) {
return false;
}
}
return true;
};两数之和 (leetcode 1)[https://leetcode-cn.com/problems/two-sum/]
- 暴力抗法,两层循环 O(n2)
1
2
3
4
5
6
7
8
9var twoSum = function (nums, target) {
for (let i = 0; i < nums.length - 1; i++) {
for (let j = i + 1; j < nums.length; j++) {
if (nums[i] + nums[j] === target) {
return [i, j];
}
}
}
};- map 解决 x+y = 9 => y = 9-x。O(n)
1
2
3
4
5
6
7
8
9
10
11var twoSum = function (nums, target) {
let hash = {};
for (let i = 0; i < nums.length; i++) {
if (hash[target - nums[i]] !== undefined) {
// 保证小的索引在前
return [i, hash[target - nums[i]]].sort((a, b) => a - b);
}
hash[nums[i]] = i;
}
return [];
};三数之和 leetcode 15
- 暴力抗法,三层循环 O(n3)。数据大直接超时。。
1
2
3
4
5
6
7
8
9
10
11
12
13var threeSum = function (nums) {
const arr = [];
for (let i = 0; i < nums.length - 2; i++) {
for (let j = i + 1; j < nums.length - 1; j++) {
for (let k = j + 1; k < nums.length; k++) {
if (nums[i] + nums[j] + nums[k] === 0) {
arr.push([nums[i], nums[j], nums[k]].sort().join(','));
}
}
}
}
return [...new Set(arr)].map((v) => v.split(','));
};- 双指针往中间夹
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32var threeSum = function (nums) {
if (nums.length < 3) {
return [];
}
nums = nums.sort();
const arr = [];
for (let i = 0; i < nums.length - 2; i++) {
if (i > 0 && nums[i] === nums[i - 1]) {
continue;
}
let left = i + 1;
let right = nums.length - 1;
while (left < right) {
if (nums[i] + nums[left] + nums[right] === 0) {
arr.push([nums[i], nums[left], nums[right]].sort().join(','));
while (left < right && nums[left] == nums[left + 1]) {
left += 1;
}
while (left < right && nums[right] == nums[right - 1]) {
right -= 1;
}
left += 1;
right -= 1;
} else if (nums[i] + nums[left] + nums[right] < 0) {
left += 1;
} else if (nums[i] + nums[left] + nums[right] > 0) {
right -= 1;
}
}
}
return [...new Set(arr)].map((v) => v.split(','));
};
树、二叉树、二叉搜索树
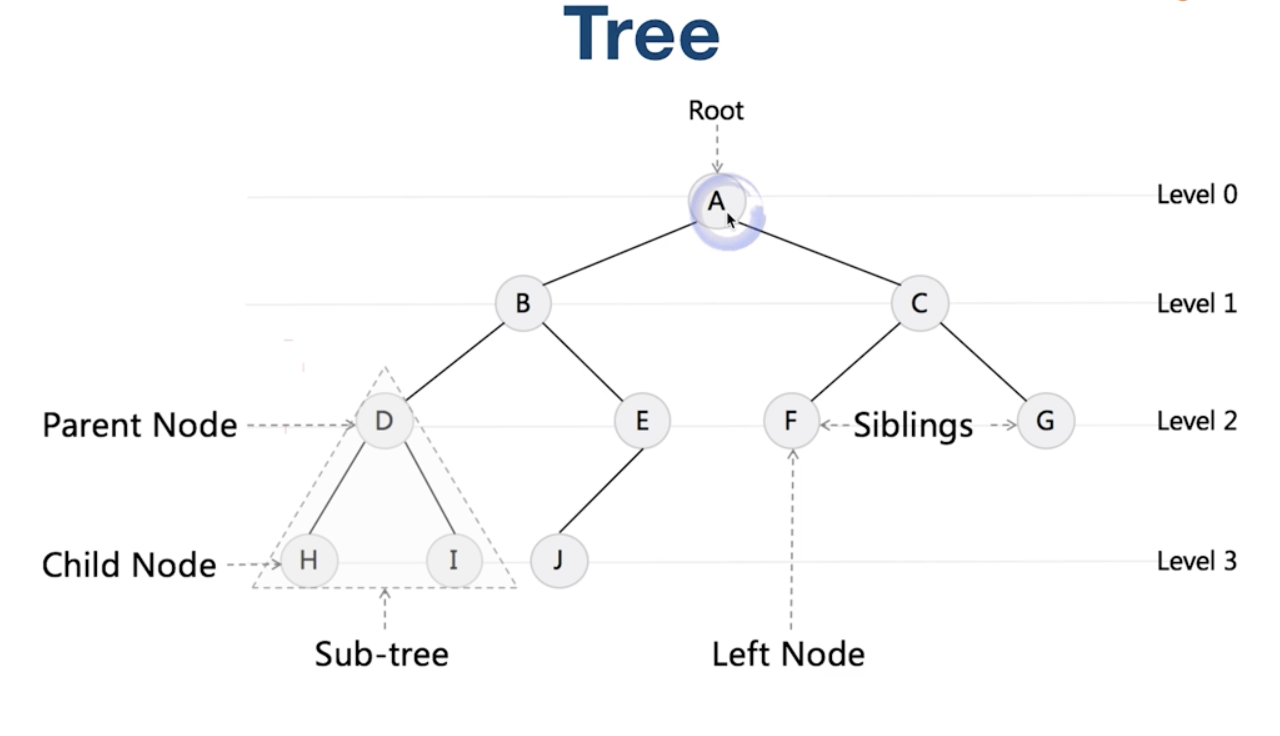
完全二叉树:每个节点要么没有子节点,要么有两个节点
二叉搜索树:左子树所有节点都小于根节点,右子树所有节点都大于根节点,递归左子树也要满足
二叉搜索树每次搜索只要找左边或者右边,效率比较高 平均 O(logn),最坏 O(n)(树不平衡)
验证二叉搜索树 (leetcode 98)[https://leetcode-cn.com/problems/validate-binary-search-tree/]
中序遍历 => 遍历后的值肯定是升序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isValidBST = function (root) {
// 升序
return inOrder(root).every((v, i, arr) => {
if (i != 0) {
return arr[i] > arr[i - 1];
}
return true;
});
};
var inOrder = function (root) {
if (root === null) {
return [];
}
return [...inOrder(root.left), root.val, ...inOrder(root.right)];
};递归。利用特性,每个节点都大于它的左节点,小于右节点。在左遍历中,最大值为根;右遍历中,最小值为根。
1
2
3
4
5
6
7
8
9
10
11
12// 限定以 root 为根的子树节点必须满足 max.val > root.val > min.val
var isValidBST = function (root, min = -Infinity, max = Infinity) {
// 如果是空节点
if (!root) return true;
// 若 root.val 不符合 max 和 min 的限制,说明不是合法 BST
if (root.val <= min || root.val >= max) return false;
// 限定左子树的最大值是 root.val,右子树的最小值是 root.val
return (
isValidBST(root.left, min, root.val) &&
isValidBST(root.right, root.val, max)
);
};二叉树最小共同祖先 leetcode 235
- 找出路径,路径最后重合的地方就是最近的公共祖先(因为没有 parent 指针,需要从跟开始找)(On)
- 递归: findPorQ(root, p, q) 找到满足 p 或者 q O(n)
1
2
3
4
5
6
7
8var lowestCommonAncestor = function (root, p, q) {
// 如果 p 是 q 的祖先或者反过来,那公共祖先就是其中之一
if (root == null || root == p || root == q) return root;
let left = lowestCommonAncestor(root.left, p, q);
let right = lowestCommonAncestor(root.right, p, q);
// 左侧没找到
return left == null ? right : right == null ? left : root;
};
二叉树遍历
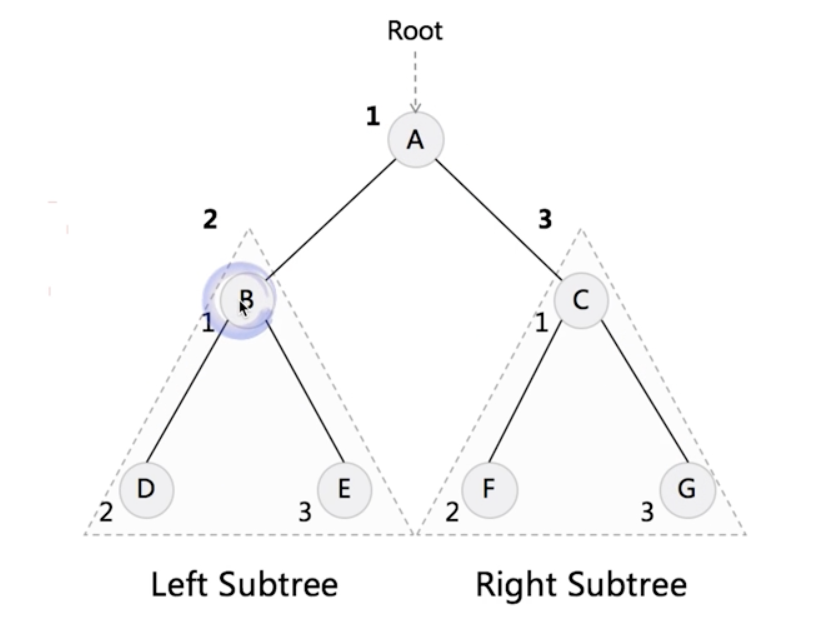
指的是根的位子
- pre-order 前序 ABDECFG
- in-order 中序 DBEAFCG
- post-order 后序 DEBFGCA

有意义的在于,二叉搜索树,中序遍历出来是有序的
递归和分治
盗梦空间 => 层层进入下一层梦,每次只能回到上一层的梦境,层层回来。
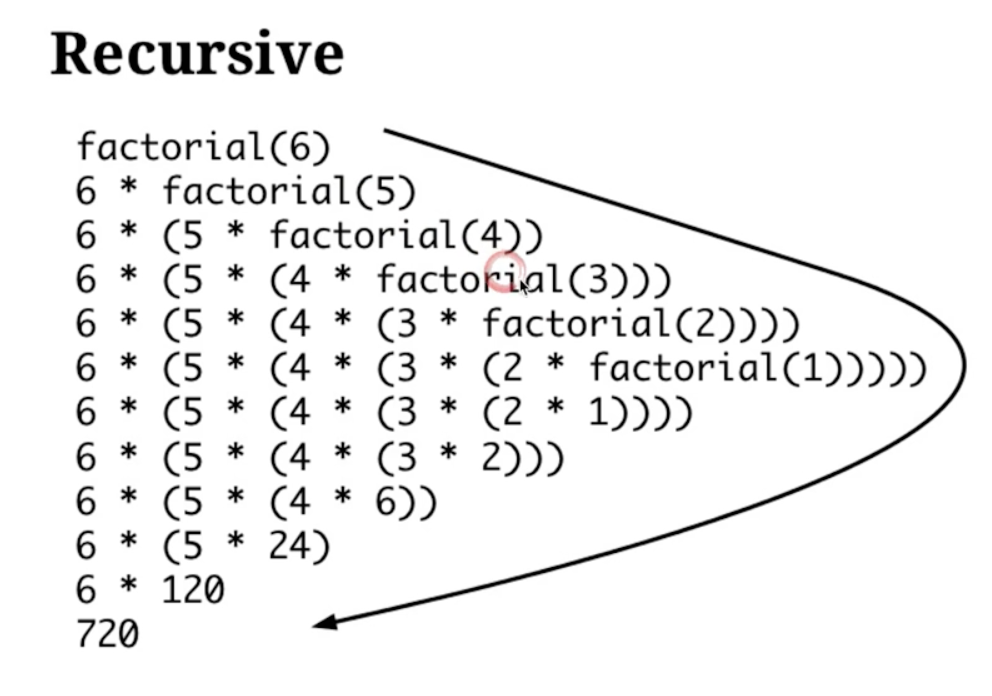
递归的模板
1 | function recursion(level, param1, param2...) { |
pow(x,n) => x^n leetcode 50
库函数 pow 和 **
暴力累乘 O(n)
递归分治,减半规模 O(logn)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15var myPow = function (x, n) {
if (n === 0) {
return 1;
}
// n 为负数
if (n < 0) {
return 1 / myPow(x, -n);
}
// n 有余数
if (n % 2) {
return x * myPow(x, n - 1);
}
// 分治
return myPow(x * x, n / 2);
};
求众数(前提是一定有)leetcode 169
- 暴力,循环每个元素的数量,再循环一次(O(n2))
- Map {x: count_x}
- 排序,重复的次数>n/2 O(nlongn)
1
2
3
4const majorityElement = (nums) => {
nums.sort((a, b) => a - b);
return nums[parseInt(nums.length / 2)];
}; - 分治
贪心算法
每次选当前最好的选择

纸币数最少的配置
但是有一定的条件。不能处处只看眼前。前提是:问题能分成子问题来解决,并且,子问题能递推到最终的最优解(最优子结构)。可遇不可求。
与动态规划的区别在于,动归能保存以前的计算结果,根据以前的结果对当前进行选择。
- 买股票的最佳时机(只能持有一股,无手续费) leetcode 122
- 每天如果后一天比前一天高,就买入,第二天卖出(On)
1
2
3
4
5
6
7
8
9var maxProfit = function (prices) {
let revenue = 0;
for (let i = 0; i < prices.length - 1; i++) {
if (prices[i] < prices[i + 1]) {
revenue += prices[i + 1] - prices[i];
}
}
return revenue;
}; - 动态规划
- 每天如果后一天比前一天高,就买入,第二天卖出(On)
广度和深度优先搜索
BFS(Breadth-First Search):广度(队列实现)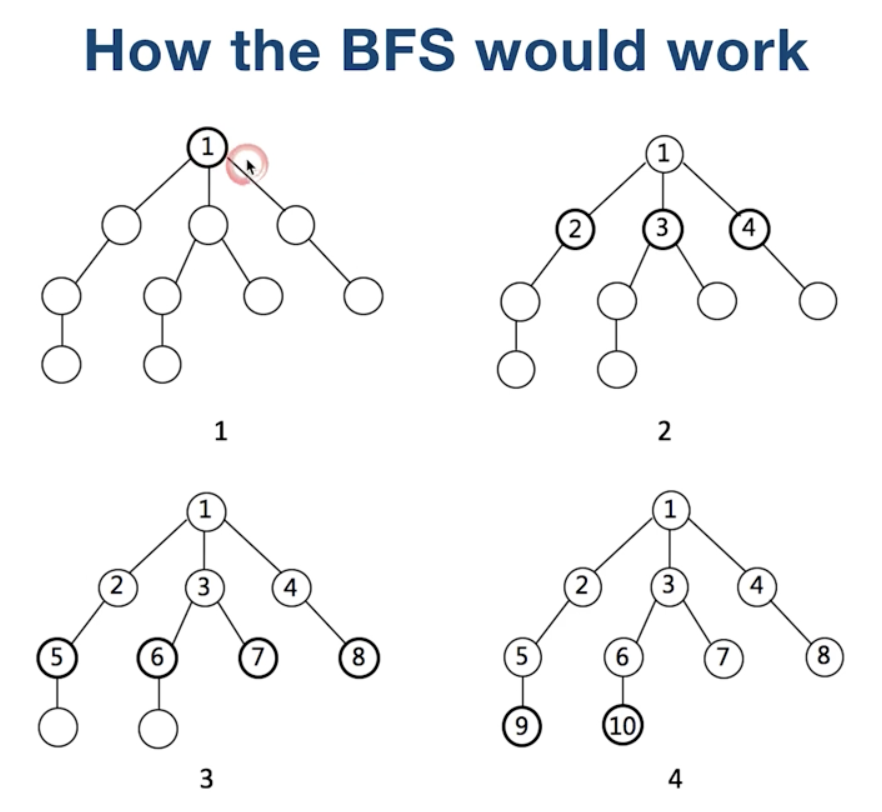
DFS(Depth-First-Search):深度(递归实现)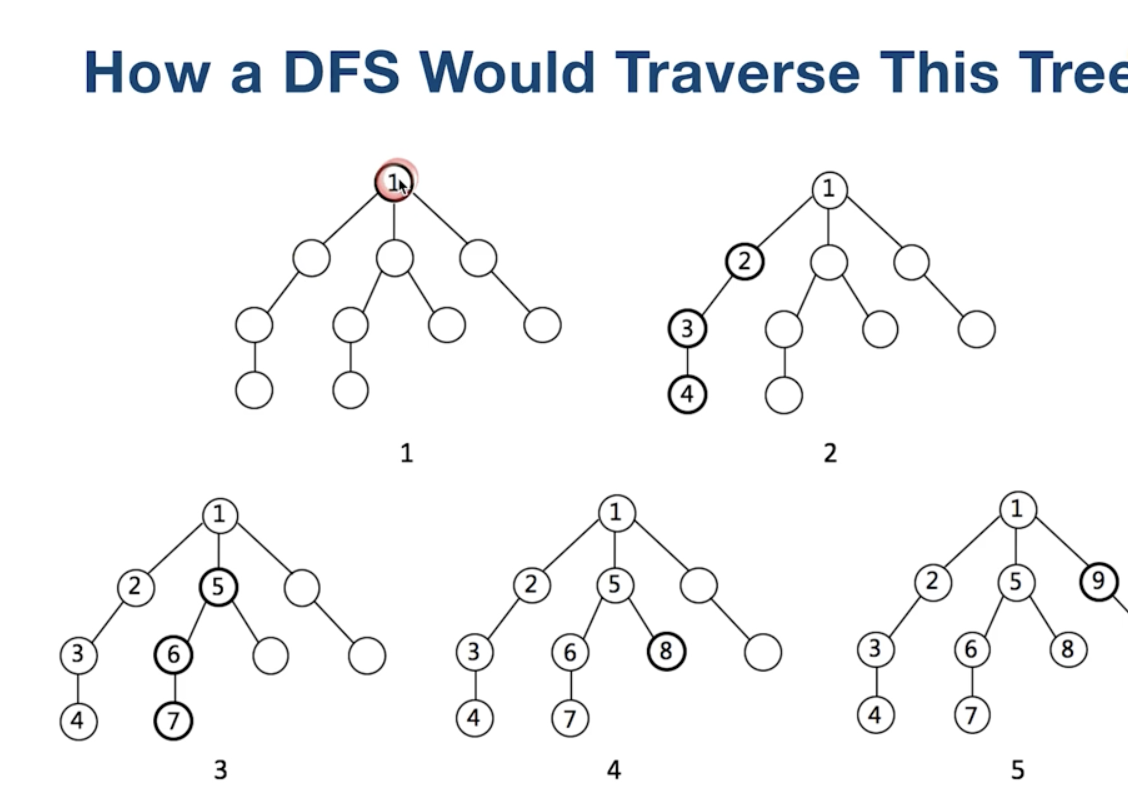
二叉树层次遍历 (leetcode)[https://leetcode-cn.com/problems/binary-tree-level-order-traversal/]
- BFS => 维护一个队列,遍历该队列的在某一层的长度,遍历完出列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23var levelOrder = function (root) {
if (root == null) {
return [];
}
let result = [];
let arr = [root];
while (arr.length) {
const level_size = arr.length;
const current = [];
for (let i = 0; i < level_size; i++) {
const node = arr.shift();
current.push(node.val);
if (node.left) {
arr.push(node.left);
}
if (node.right) {
arr.push(node.right);
}
}
result.push(current);
}
return result;
};- DFS 深度遍历 => 递归+1
1
2
3
4var maxDepth = function (root) {
if (root == null) return 0;
return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
};二叉树最大深度 leetcode 104
BFS O(n) 直接遍历,level 记录深度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20var maxDepth = function (root) {
if (root == null) return 0;
let level = 0;
let arr = [root];
// 遍历节点
while (arr.length) {
const level_size = arr.length;
level += 1;
for (let i = 0; i < level_size; i++) {
const node = arr.shift();
if (node.left) {
arr.push(node.left);
}
if (node.right) {
arr.push(node.right);
}
}
}
return level;
};DFS O(n) 直接遍历,level 记录深度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20var maxDepth = function (root) {
if (root == null) return 0;
let level = 0;
let arr = [root];
// 遍历节点
while (arr.length) {
const level_size = arr.length;
level += 1;
for (let i = 0; i < level_size; i++) {
const node = arr.shift();
if (node.left) {
arr.push(node.left);
}
if (node.right) {
arr.push(node.right);
}
}
}
return level;
};生成有效括号组合 leetcode 22
- DFS => 2n 个格子,每个格子两个选择。2^2n
- 改进:剪枝局部不合法,不再递归;left_used,right_used
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18var generateParenthesis = function (n) {
let result = [];
_gen(n, 0, 0, '', result);
return result;
};
var _gen = function (n, left, right, str, result) {
if (left === n && right === n) {
result.push(str);
return;
}
if (left < n) {
_gen(n, left + 1, right, str + '(', result);
}
if (right < left) {
_gen(n, left, right + 1, str + ')', result);
}
};
剪枝
搜索的优化策略:找局部最优的一个或者几个分支,淘汰无用的分支
脑子里其实就在推演,我如果下这里,对方会怎么下,但是人脑的链路栈是有限的,容易乱。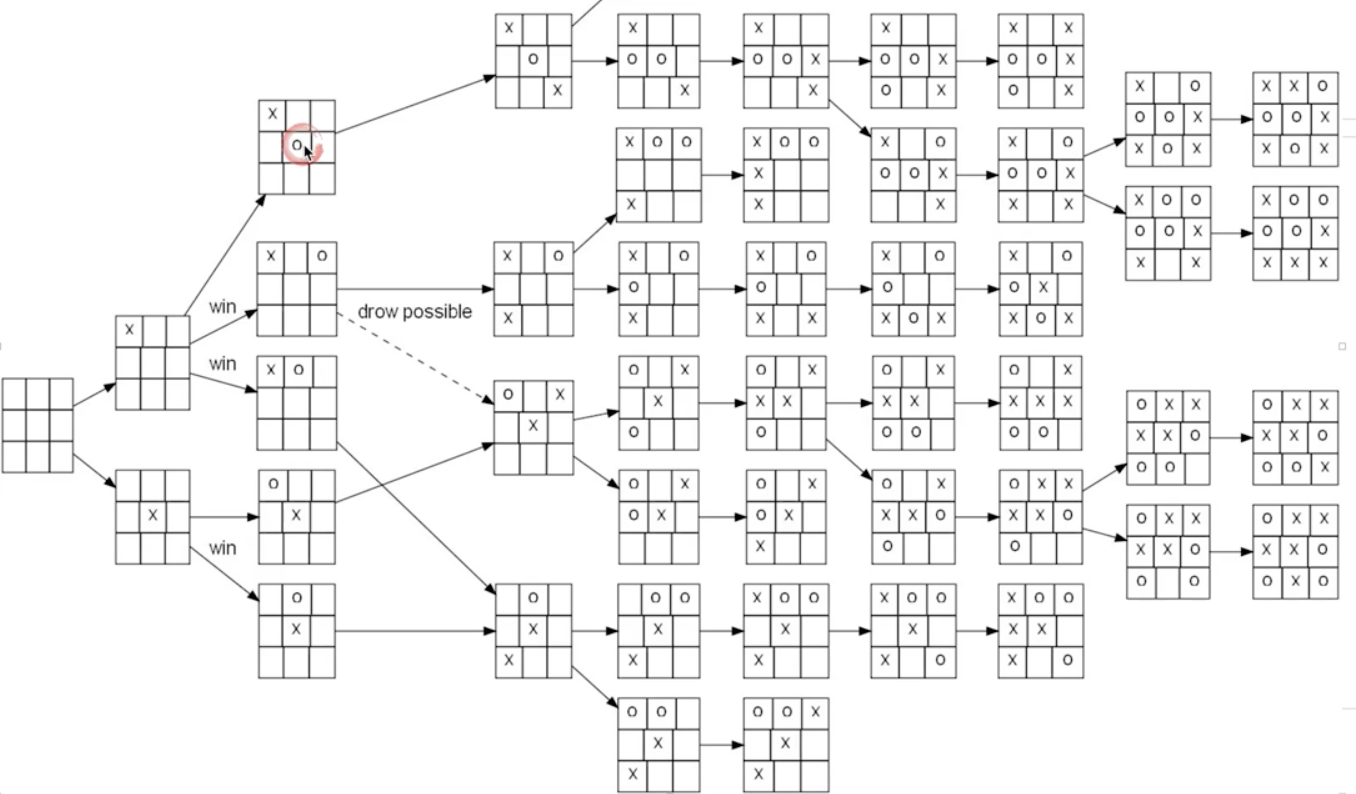
N 皇后 leetcode 51
- 用一个 set 记录不可能的格子,下次就不往这边走。关键条件,递归出口:一行最多摆一个。n 个皇后放置在 n×n 的棋盘上,那么每行至少有一个,只有走到最后一行,才会 push 到结果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42let cols = new Set();
// 被占的斜向
let pie = new Set();
// 被占的斜向
let na = new Set();
var solveNQueens = function (n) {
if (n === 0) {
return [];
}
// 记录结果
let result = [];
// 被占的列
_dfs(n, 0, [], result);
return result.map(translate);
};
// 遍历
var _dfs = function (n, row, current_state, result) {
// 最后一行
if (row >= n) {
result.push(current_state);
return;
}
for (let i = 0; i < n; i++) {
// 是否在里面
if (cols.has(i) || pie.has(row + i) || na.has(row - i)) {
continue;
}
cols.add(i);
pie.add(row + i);
na.add(row - i);
_dfs(n, row + 1, [...current_state, i], result);
cols.delete(i);
pie.delete(row + i);
na.delete(row - i);
}
};
function translate(arr) {
return arr.map(
(v) => '.'.repeat(v) + 'Q' + '.'.repeat(arr.length - v - 1)
);
}
二分查找
在选择排序的优化里面就有用到。
- 单调递增或递减(有序)
- 有界
- 能够用索引访问
- 求解平方根 leetcode 69
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25var mySqrt = function (x, n = 0) {
if (x === 0 || x === 1) {
return x;
}
let left = 0;
let right = x;
let num = 0;
while (left < right) {
let mid = (right - left) / 2 + left;
if (right - left < 10 ** -10) {
num = mid;
break;
}
const res = mid * mid;
if (res > x) {
right = mid - 1;
} else if (res < x) {
left = mid + 1;
} else {
num = mid;
break;
}
}
return num.toFixed();
};
字典树
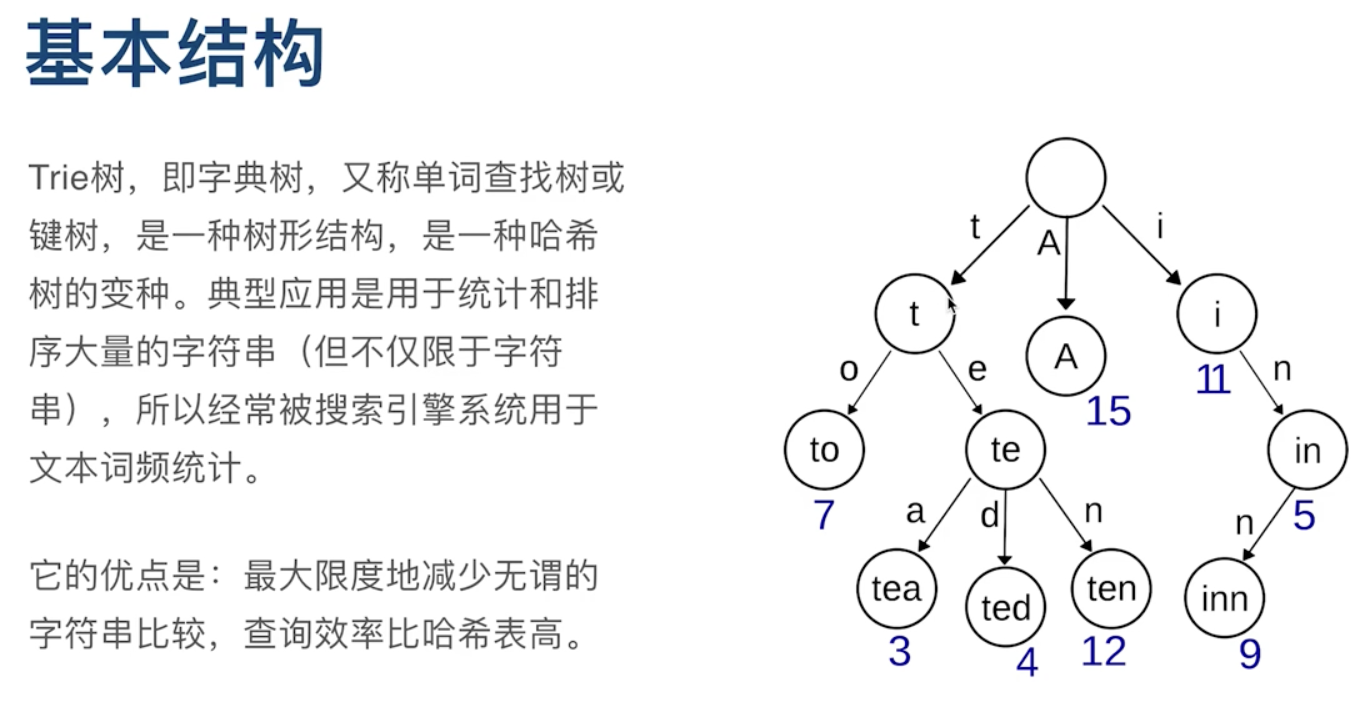 1. 实现字典树
2. 二维网格中的单词搜索问题
1. 实现字典树
2. 二维网格中的单词搜索问题
位运算
计算机用二进制存储和计算,用二进制处理速度较快。
异或的特点:

统计位 1 的个数 leetcode 191
- 转换成二进制,遍历
- & n-1, 消除最低位
1
2
3
4
5
6
7
8var hammingWeight = function (n) {
let count = 0;
while (n) {
n &= n - 1;
count++;
}
return count;
};
2 的幂次方问题 & 比特位技术问题 leetcode 231
- 一直模 2
1
2
3
4
5
6
7
8
9var isPowerOfTwo = function (n) {
if (n === 1) {
return true;
}
while (n >= 2) {
n /= 2;
}
return n === 1;
};二进制位有且只有一个 1
1
2
3var isPowerOfTwo = function (n) {
return n > 0 && (n & (n - 1)) === 0;
};N 皇后问题 => 用位运算
动态规划
动态递归。
- 递归+记忆化
- 状态定义:opt[n],dp[n],fib[n]…
- 状态转移:opt[n] = best_of(opt[n-1], opt[n-2]….)
- 最优子结构
爬楼梯 leetcode 70
- 回溯
- 递推 f(n) = f(n-1) + f(n-2)
1
2
3
4
5
6
7
8
9
10
11
12var climbStairs = function (n) {
if (n <= 2) {
return n;
}
let arr = [];
arr[0] = 1;
arr[1] = 2;
for (let i = 2; i < n; i++) {
arr[i] = arr[i - 1] + arr[i - 2];
}
return arr[n - 1];
};
三角形自顶向下的最小路径和 leetcode 120
- 递推:min = mini[j] = triangle[i][j] + Math.min(mini[j], mini[j + 1]);
1
2
3
4
5
6
7
8
9
10var minimumTotal = function (triangle) {
const mini = triangle[triangle.length - 1];
for (let i = triangle.length - 2; i >= 0; i--) {
for (let j = 0; j < triangle[i].length; j++) {
mini[j] = triangle[i][j] + Math.min(mini[j], mini[j + 1]);
}
}
return mini[0];
};乘积最大子数组 leetcode 152
股票买卖
并查集
岛屿个数&朋友圈 leetcode 200
- 染色法,找到一个 1 后,遍历周围的所有 1,把他变成 0。完成一次遍历记录为 1 个岛屿
- 并查集,遍历节点,相邻的融合,最后看有几个集合
LRU cache
缓存特点:
- 类似于记忆:容量体积小,会丢,要一直记住就要记在笔记本。
- 类似于钱包:经常要用的就要带在钱包,否则放在储物柜
CPU 缓存结构: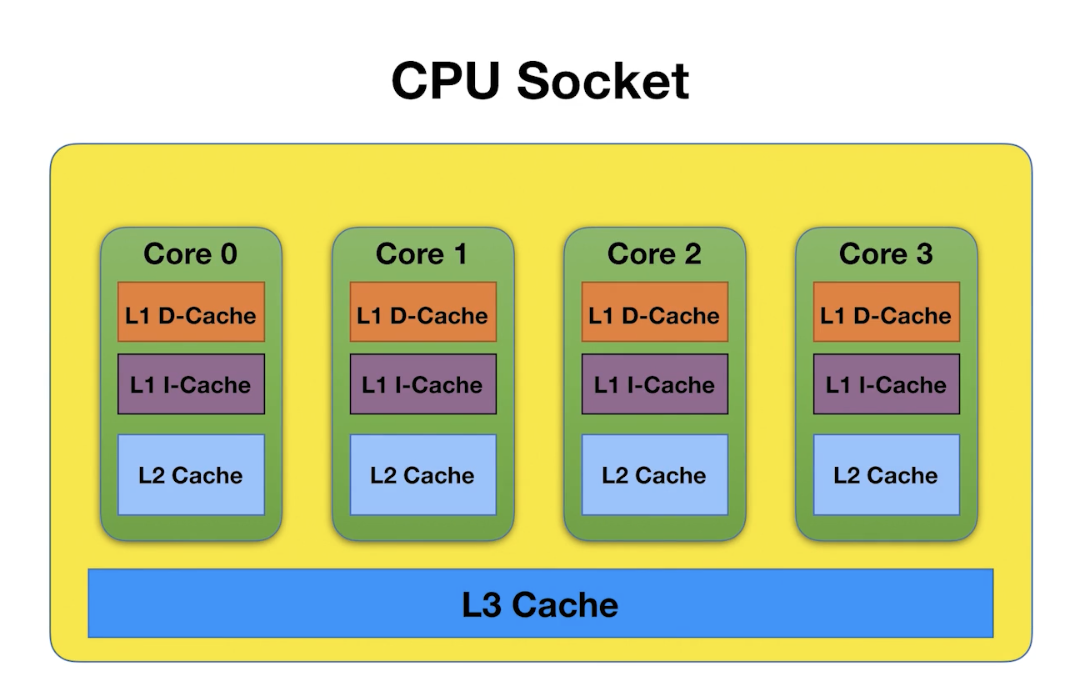
LRU 指的是缓存替换算法 Least recently used。
一般用双向链表。只查最前(最常用元素)和最后(最久没使用的元素)。
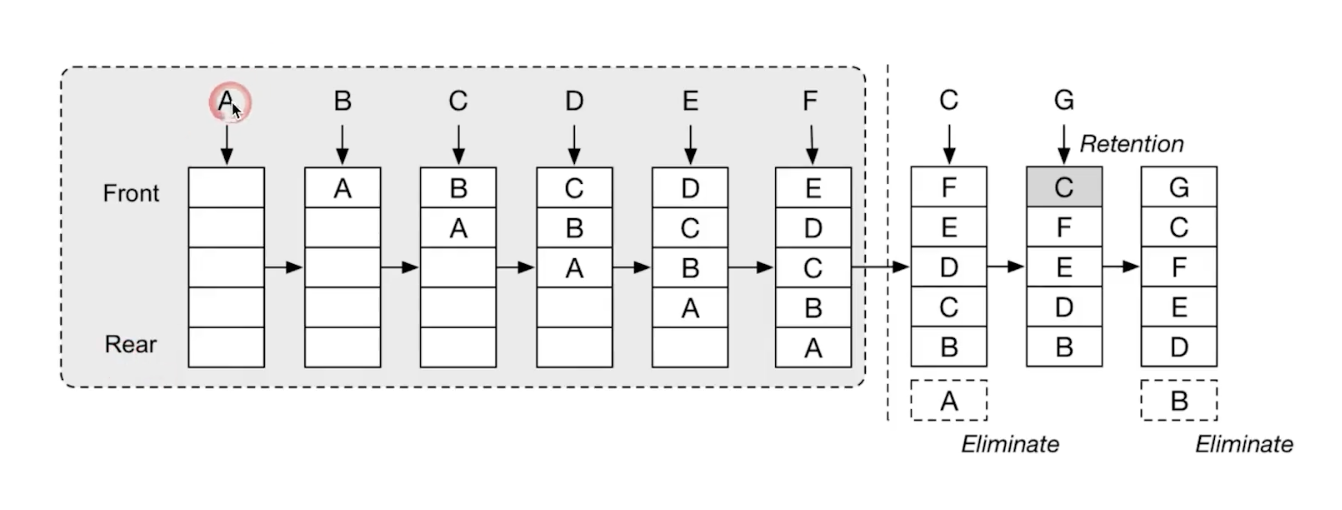
- 实现 LRU cache leetcode 146
布隆过滤器 Bloom Filter
将一个元素经过计算函数计算,散列在二进制向量中。用于检测元素是否在一个集合中。
如果未检测到,那元素肯定不存在;如果检测到了,那元素可能存在。
缺点是误识别和删除困难。
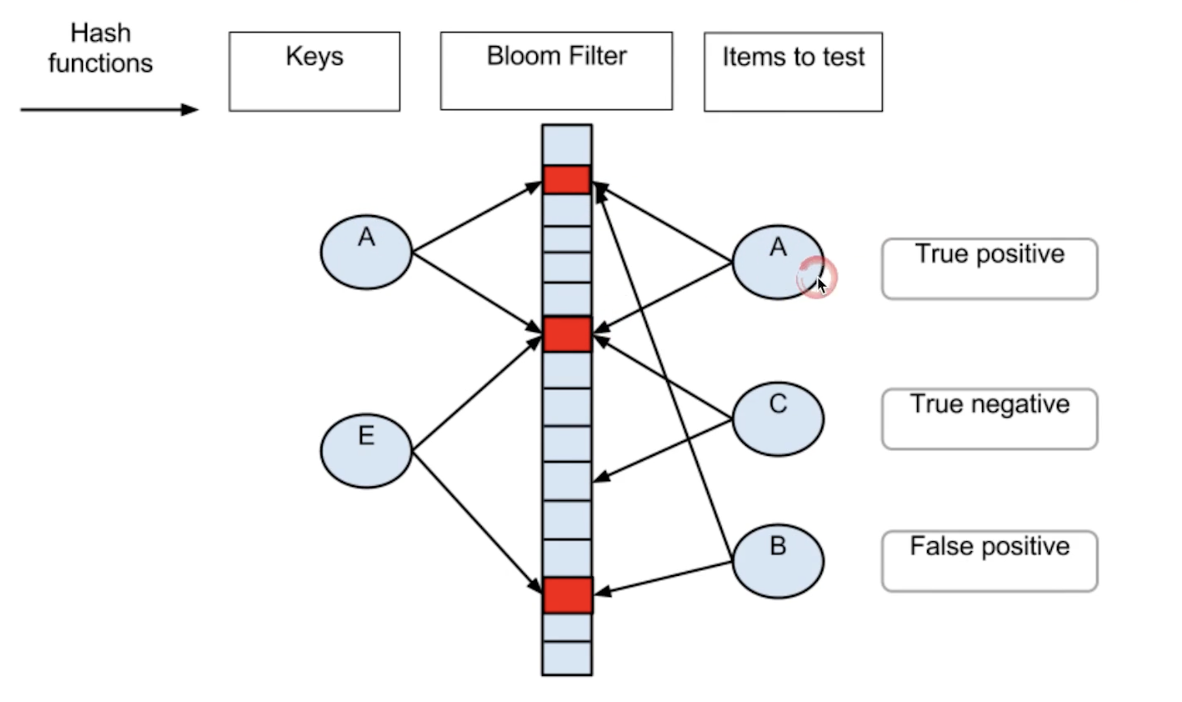
如图:A 和 E 先插入到布朗过滤器。
- A 发现是存在的
- C 发现没有完全重合的元素,说明是不存在的。
- B 发现有重合部分,会误判为存在,但其实不存在 B
常用的记忆模板
常用的几种算法思路模板,要记下来,但不是硬套。有助于整理思路。
1. 递归
1 | function recursion(level, param1, param2) { |
2. DFS => 递归
1 | visited = set() |
3. BFS
1 | def BFS(graph, start, end) : |
4. 二分查找
1 | left, (right = 0), arr.length - 1 |
5. DP 动规
1 | // 状态定义 |
以上
看到题目的时候,首先要想,最蠢的办法是什么。
一般来说,最简单的暴力解法就是递归、循环、穷举,这些方法的事件空间复杂度往往会很高。
然后再想有什么数据结构可以解决,一般会比暴力抗法事件复杂度低。
最后再进行边角的优化,剪枝、缓存等等,减少一定的量级。
